
【题目】已知函数![]() .
.
(1)讨论![]() 极值点的个数;
极值点的个数;
(2)若![]() 是
是![]() 的一个极值点,且
的一个极值点,且![]() ,证明:
,证明: ![]() .
.
【答案】(1) 当![]() 时,
时,![]() 无极值点;当
无极值点;当![]() 时,
时,![]() 有
有![]() 个极值点;当
个极值点;当![]() 或
或![]() 时,
时,![]() 有
有![]() 个极值点;(2)证明见解析
个极值点;(2)证明见解析
【解析】
(1)求导得到![]() ;分别在
;分别在![]() 、
、![]() 、
、![]() 和
和![]() 四种情况下根据
四种情况下根据![]() 的符号确定
的符号确定![]() 的单调性,根据极值点定义得到每种情况下极值点的个数;(2)由(1)的结论和
的单调性,根据极值点定义得到每种情况下极值点的个数;(2)由(1)的结论和![]() 可求得
可求得![]() ,从而得到
,从而得到![]() ,代入函数解析式可得
,代入函数解析式可得![]() ;令
;令![]() 可将
可将![]() 化为关于
化为关于![]() 的函数
的函数![]() ,利用导数可求得
,利用导数可求得![]() 的单调性,从而得到
的单调性,从而得到![]() ,进而得到结论.
,进而得到结论.
(1)![]()
①当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增
上单调递增
![]() 为
为![]() 的唯一极小值点,无极大值点,即此时
的唯一极小值点,无极大值点,即此时![]() 极值点个数为:
极值点个数为:![]() 个
个
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,![]()
⑴当![]() 时,
时,![]()
![]() 和
和![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]() 在
在![]() ,
,![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
![]() 为
为![]() 的极大值点,
的极大值点,![]() 为
为![]() 的极小值点,即
的极小值点,即![]() 极值点个数为:
极值点个数为:![]() 个
个
⑵当![]() 时,
时,![]() ,此时
,此时![]() 恒成立且不恒为
恒成立且不恒为![]()
![]() 在
在![]() 上单调递增,无极值点,即
上单调递增,无极值点,即![]() 极值点个数为:
极值点个数为:![]() 个
个
⑶当![]() 时,
时,![]()
![]() 和
和![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]() 在
在![]() ,
,![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
![]() 为
为![]() 的极大值点,
的极大值点,![]() 为
为![]() 的极小值点,即
的极小值点,即![]() 极值点个数为:
极值点个数为:![]() 个
个
综上所述:当![]() 时,
时,![]() 无极值点;当
无极值点;当![]() 时,
时,![]() 有
有![]() 个极值点;当
个极值点;当![]() 或
或![]() 时,
时,![]() 有
有![]() 个极值点
个极值点
(2)由(1)知,若![]() 是
是![]() 的一个极值点,则
的一个极值点,则![]()
又![]() ,即
,即![]()
![]()
![]()
![]()
![]() 令
令![]() ,则
,则![]()
![]() ,
,![]()
则![]()
当![]() 时,
时,![]() ,
,![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
![]() ,即
,即![]()
![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点.
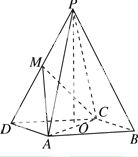
(1)证明:PB∥平面ACM;
(2)证明:AD⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=1,b1=﹣1,a2-b2=2.
(1)若a3-b3=6,求{bn}的通项公式
(2)若T3=﹣13,求S5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明设计了一款正四棱锥形状的包装盒,如图所示,![]() 是边长为
是边长为![]() 的正方形硬纸片,切去阴影部分所示的四个全等的等腰三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰三角形,再沿虚线折起,使得![]() 四个点重合于图中的点
四个点重合于图中的点![]() ,正好形成一个正四棱锥形状的包装盒,设正四棱锥底面正方形的边长为
,正好形成一个正四棱锥形状的包装盒,设正四棱锥底面正方形的边长为![]()
![]() .
.

(1)试用![]() 表示该四棱锥的高度
表示该四棱锥的高度![]() ,并指出
,并指出![]() 的取值范围;
的取值范围;
(2)若要求侧面积不小于![]() ,求该四棱锥的高度的最大值,并指出此时该包装盒的容积.
,求该四棱锥的高度的最大值,并指出此时该包装盒的容积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养路处建造圆锥形仓库用于贮藏食盐已建的仓库的底面直径为![]() ,高
,高![]() ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大![]() (高不变);二是高度增加
(高不变);二是高度增加![]() ,(底面直径不变).
,(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校实行自主招生,参加自主招生的学生从8个试题中随机挑选出4个进行作答,至少答对3个才能通过初试已知甲、乙两人参加初试,在这8个试题中甲能答对6个,乙能答对每个试题的概率为![]() ,且甲、乙两人是否答对每个试题互不影响.
,且甲、乙两人是否答对每个试题互不影响.
(1)试通过概率计算,分析甲、乙两人谁通过自主招生初试的可能性更大;
(2)若答对一题得5分,答错或不答得0分,记乙答题的得分为![]() ,求
,求![]() 的分布列及数学期望和方差.
的分布列及数学期望和方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com