
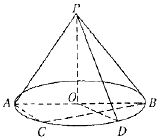
 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.分析 (Ⅰ)证法1:设BC∩OD=E,由已知可证AC∥OE,线线平行即可证明线面平行AC∥平面POD;证法2:由AB是底面圆的直径,可证AC⊥BC,利用OD⊥BC,可证AC∥OD,即可判定AC∥平面POD.
(Ⅱ)设圆锥底面半径为r,高为h,母线长为l,由圆锥的轴截面PAB为等腰直角三角形,可求$h=r,l=\sqrt{2}r$,利用三角形面积公式可求r,进而可求此圆锥的表面积.
解答 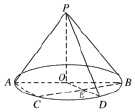 解:(Ⅰ)证法1:设BC∩OD=E,∵D是弧BC的中点,
解:(Ⅰ)证法1:设BC∩OD=E,∵D是弧BC的中点,
∴E是BC的中点,
又∵O是AB的中点,∴AC∥OE,
又∵AC?平面POD,OE?平面POD,
∴AC∥平面POD.
证法2:∵AB是底面圆的直径,∴AC⊥BC,
∵弧BC的中点为D,∴OD⊥BC,
又AC,OD共面,∴AC∥OD,
又AC?平面POD,OD?平面POD,
∴AC∥平面POD.
(Ⅱ)解:设圆锥底面半径为r,高为h,母线长为l,
∵圆锥的轴截面PAB为等腰直角三角形,
∴$h=r,l=\sqrt{2}r$,
∵由${S_{△ABC}}=\frac{1}{2}×2r×h={r^2}=9$,得r=3,
∴${S_表}=πrl+π{r^2}=πr×\sqrt{2}r+π{r^2}=9({1+\sqrt{2}})π$.
点评 本题主要考查了线面平行的判定,考查了三角形面积公式,考查了圆锥的表面积的求法,考查了空间想象能力和推理论证能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 44 | C. | 46 | D. | 47 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | i>9 | B. | i<9 | C. | i>18 | D. | i<18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a=m,b=m | B. | b=m,a=m | C. | a=f(m),b=f(m) | D. | b=f(m),a=f(m) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲射击的平均成绩比乙好 | |
| B. | 乙射击的平均成绩比甲好 | |
| C. | 甲射击的成绩的众数小于乙射击的成绩的众数 | |
| D. | 甲射击的成绩的极差大于乙射击的成绩的极差 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com