

| A. | i>9 | B. | i<9 | C. | i>18 | D. | i<18 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S的值,模拟循环过程可得条件.
解答 解:程序运行过程中,各变量值如下表所示:
S=0,n=2,i=1
不满足条件,第一圈:S=0+$\frac{1}{2}$,n=4,i=2,
不满足条件,第二圈:S=$\frac{1}{2}$+$\frac{1}{4}$,n=6,i=3,
不满足条件,第三圈:S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$,n=8,i=4,
…
依此类推,
不满足条件,第8圈:S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$++…+,n=18,i=9,
不满足条件,第9圈:S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$++…+$\frac{1}{18}$,n=20,i=10,
此时,应该满足条件,退出循环
其中判断框内应填入的条件是:i>9.
故选:A.
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误,属于基础题.


科目:高中数学 来源: 题型:解答题
| 分组 | [25,35) | [35,45) | [4,55) | [55,65) | [65,75) | [75,85) | [85,95) |
| 甲厂频数 | 10 | 40 | 115 | 165 | 120 | 45 | 5 |
| 乙厂频数 | 5 | 60 | 110 | 160 | 90 | 70 | 5 |
| P(k2≥k) | 0.05 | 0.01 | 0.001 |
| h | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
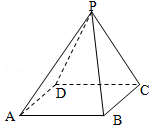 如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )| A. | 4 | B. | 8 | C. | 12π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{{x^2}+1}}>\frac{1}{{{y^2}+1}}$ | B. | ln(x2+1)>ln(y2+1) | C. | sinx>siny | D. | x3>y3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
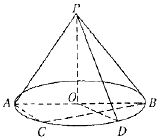 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
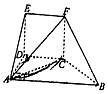 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .y=sin2x | B. | .y=-sin2x | C. | .y=cos2x | D. | y=-2cosx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com