
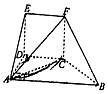
 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.分析 (Ⅰ)证明AC⊥BC.DE⊥BC.推出CF⊥BC.即可证明BC⊥平面ACF.然后推出BC⊥AF.
(Ⅱ)利用V几何体EF-ABCD=V几何体A-CDEF+V几何体F-ACB,求解即可.
解答 (Ⅰ)证明:因为△ACB是腰长为$2\sqrt{2}$的等腰直角三角形,所以AC⊥BC.
因为DE⊥平面ABCD,所以DE⊥BC.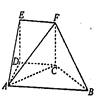
又DE∥CF,所以CF⊥BC.
又AC∩CF=C,所以BC⊥平面ACF.
所以BC⊥AF.
(Ⅱ)解:因为△ABC是腰长为$2\sqrt{2}$的等腰直角三角形,
所以$AC=BC=2\sqrt{2},AB=\sqrt{A{C^2}+B{C^2}}=4$,
所以$AD=BCsin∠ABC=2\sqrt{2}×sin45°=2,CD=AB=BCcos∠ABC=4-2\sqrt{2}×cos45°=2$.
所以DE=EF=CF=2,
由勾股定理得$AE=\sqrt{A{D^2}+D{E^2}}=2\sqrt{2}$,
因为DE⊥平面ABCD,所以DE⊥AD.
又AD⊥DC,DE∩DC=D,所以AD⊥平面CDEF.
所以V几何体EF-ABCD=V几何体A-CDEF+V几何体F-ACB=$\frac{1}{3}{S_{四边形CDEF}}•AD+\frac{1}{3}{S_{△ABC}}•CF$=$\frac{1}{3}CD•DE•AD+\frac{1}{3}•\frac{1}{2}AC•BC•CF$=$\frac{1}{3}×2×2×2+\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×2\sqrt{2}×2$=$\frac{16}{3}$.
点评 本题考查直线与平面垂直的判定定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | i>9 | B. | i<9 | C. | i>18 | D. | i<18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲射击的平均成绩比乙好 | |
| B. | 乙射击的平均成绩比甲好 | |
| C. | 甲射击的成绩的众数小于乙射击的成绩的众数 | |
| D. | 甲射击的成绩的极差大于乙射击的成绩的极差 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{-3+\sqrt{17}}}{2}$ | B. | $\frac{{3-\sqrt{17}}}{2}$ | C. | $\frac{{-3±\sqrt{17}}}{2}$ | D. | $\frac{{3±\sqrt{17}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com