练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一鲜花店根据一个月（30天）某种鲜花的日销售量与销售天数统计如下，将日销售量落入各组区间频率视为概率．

    日销售量（枝）

    销售天数

    3天

    5天

    13天

    6天

    3天

    （1）试求这30天中日销售量低于100枝的概率；

    （2）若此花店在日销售量低于100枝的时候选择2天作促销活动，求这2天恰好是在日销售量低于50枝时的概率．

    【答案】（1）;（2）．

    【解析】试题分析: （1）设月销量为,分别计算出和的概率,相加即可;（2）日销售量低于100枝共有8天，从中任选两天促销共有种情况; 日销售量低于50枝共有3天，从中任选两天促销共有种情况,根据古典概率计算即可.

    试题解析:（1）设月销量为，则，，

    ∴．

    （2）日销售量低于100枝共有8天，从中任选两天促销共有种情况；日销售量低于50枝共有3天，从中任选两天促销共有种情况．

    由古典概型公式得：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设Sn是数列{an}的前n项和，且2an+Sn=An2+Bn+C．
    （1）当A=B=0，C=1时，求an；
    （2）若数列{an}为等差数列，且A=1，C=﹣2． ①设bn=2nan ， 求数列{bn}的前n项和；
    ②设cn= ，若不等式cn≥ 对任意n∈N*恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在原点，焦点在轴，焦距为2，且长轴长是短轴长的倍．

    （1）求椭圆的标准方程；

    （2）设，过椭圆左焦点的直线交于、两点，若对满足条件的任意直线，不等式（）恒成立，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是某赛季甲、乙两名篮球运动员参加的每场比赛得分的茎叶图，由甲、乙两人这几场比赛得分的中位数之和是（ ）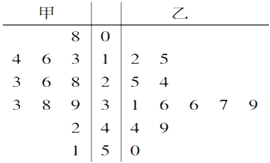
    A.65
    B.64
    C.63
    D.62

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左右焦点分别为，点为椭圆上一点. 的重心为，内心为，且，则该椭圆的离心率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据

    房屋面积（平方米）

    115

    110

    80

    135

    105

    销售价格（万元）

    24.8

    21.6

    18.4

    29.2

    22


    （1）画出散点图
    （2）求线性回归方程
    （3）根据（2）的结果估计房屋面积为150平方米时的销售价格．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A，B两种不同的教学方式分别在甲、乙两个班进行教改实验．为了了解教学效果，期末考试后，陈老师对甲、乙两个班级的学生成绩进行统计分析，画出频率分布直方图(如下图)．记成绩不低于90分者为“成绩优秀”．

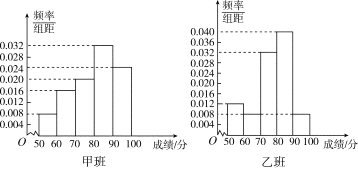
    （Ⅰ）根据频率分布直方图填写下面2×2列联表；

    甲班(A方式)

    乙班(B方式)

    总计

    成绩优秀

    成绩不优秀

    总计

    （Ⅱ）判断能否在犯错误的概率不超过0.05的前提下认为：“成绩优秀”与教学方式有关？

    附：.

    P(K2≥k)

    0.25

    0.15

    0.10

    0.05

    0.025

    k

    1.323

    2.072

    2.706

    3.841

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    若，求函数的极值；

    设函数，求函数的单调区间；

    若在区间上不存在，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的单调区间与极值；

    （2）当时，令，若在上有两个零点，求实数的取值范围；

    （3）当时，函数的图像上所有点都在不等式组所表示的平面区域内，求实数a的取值范围.

    查看答案和解析>>

    同步练习册答案