
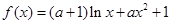 .
.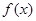 的单调性;
的单调性; 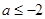 ,证明:对任意
,证明:对任意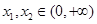 ,
,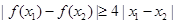 .
.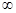 ),
),
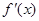 >0,故f(x)在(0,+
>0,故f(x)在(0,+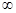 )单调增加;
)单调增加;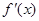 <0, 故f(x)在(0,+
<0, 故f(x)在(0,+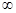 )单调减少;
)单调减少;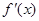 =0,解得x=
=0,解得x=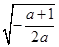 .当x∈(0,
.当x∈(0, 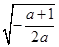 )时,
)时, 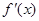 >0;
>0;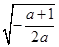 ,+
,+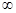 )时,
)时,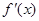 <0, 故f(x)在(0,
<0, 故f(x)在(0, 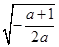 )单调增加,在(
)单调增加,在(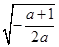 ,+
,+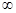 )单调减少
)单调减少 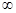 )单调减少.
)单调减少.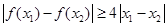 等价于
等价于 ≥4x1-4x2,
≥4x1-4x2,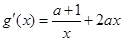 +4=
+4=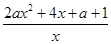 .
. 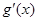 ≤
≤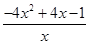 =
=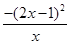 ≤0.
≤0.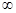 )单调减少,故g(x1) ≤g(x2),即 f(x1)+ 4x1≤f(x2)+ 4x2,
)单调减少,故g(x1) ≤g(x2),即 f(x1)+ 4x1≤f(x2)+ 4x2,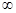 ) ,
) ,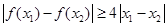 .
.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源:不详 题型:填空题
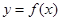 满足:
满足: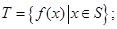 (ii)对任意
(ii)对任意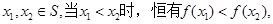
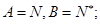
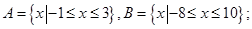
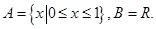
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的最大允许值是多少?
的最大允许值是多少? 达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
达到最大而实际投入又不超过预算,正面铁栅应设计为多长?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
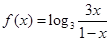 .
. 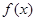 的图像关于点
的图像关于点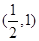 对称;
对称;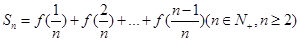 ,求
,求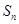 ;
;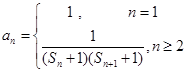
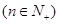 ,
,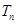 为数列
为数列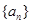 的前
的前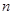 项和,若
项和,若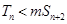 对一切
对一切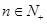 都成立,试求实数
都成立,试求实数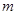 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com