
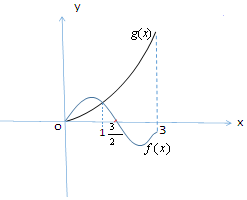
 已知函数y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域是[-3,3],它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)≥0的解集是[-3,-$\frac{3}{2}$]∪[0,$\frac{3}{2}$].
已知函数y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域是[-3,3],它们在x∈[0,3]上的图象如图所示,则不等式f(x)•g(x)≥0的解集是[-3,-$\frac{3}{2}$]∪[0,$\frac{3}{2}$]. 分析 根据函数奇偶性的性质,分别求出不等式对应的解集,进行分类讨论进行求解即可.
解答 解:∵y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],
∴由图象知,f(x)>0得解集为(0,$\frac{3}{2}$)∪(-$\frac{3}{2}$,0),f(x)<0得解集为($\frac{3}{2}$,3)∪(-3,$\frac{3}{2}$),
g(x)>0得解集为(0,3),g(x)<0得解集为(-3,0),
若f(x)•g(x)≥0,
则$\left\{\begin{array}{l}{f(x)≥0}\\{g(x)≥0}\end{array}\right.$或$\left\{\begin{array}{l}{f(x)≤0}\\{g(x)≤0}\end{array}\right.$,
即0≤x≤$\frac{3}{2}$或-3≤x≤-$\frac{3}{2}$,
即不等式f(x)•g(x)≥0的解集为[-3,-$\frac{3}{2}$]∪[0,$\frac{3}{2}$],
故答案为[-3,-$\frac{3}{2}$]∪[0,$\frac{3}{2}$].
点评 本题主要考查不等式的求解,根据函数奇偶性的性质以及数形结合是解决本题的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,△ABC中,D为AC的中点,AB=2,BC=$\sqrt{7}$,∠A=$\frac{π}{3}$.
如图所示,△ABC中,D为AC的中点,AB=2,BC=$\sqrt{7}$,∠A=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com