
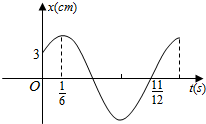
 如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求:
如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求:分析 (1)求出解析式中的参数,即可求出函数解析式;
(2)A=6,可得单摆摆动到最右边时,离开平衡位置的距离;
(3)T=1,可得单摆来回摆动一次需要的时间.
解答 解:(1)由题意,$\frac{11}{12}$-$\frac{1}{6}$=$\frac{3}{4}$T,∴T=1,
∴$\frac{2π}{ω}$=1,∴ω=2π,
∵t=$\frac{1}{6}$,s最大,
∴2π•$\frac{1}{6}$+φ=$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,
∵t=0,s=3,
∴A=6,
∴s=6sin(2πt+$\frac{π}{6}$);
(2)A=6,单摆摆动到最右边时,离开平衡位置的距离是6cm;
(3)T=1,单摆来回摆动一次需要1s.
点评 本题考查三角函数的解析式的求法与应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份 | 9 | 10 | 11 | 12 | 1 |
| 历史(x分) | 79 | 81 | 83 | 85 | 87 |
| 政治(y分) | 77 | 79 | 79 | 82 | 83 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{23}{27}$,1] | B. | [-$\frac{23}{27}$,1] | C. | [1,3] | D. | (-∞1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | [-3,-1] | C. | [-3,1] | D. | [1,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com