
| 月份 | 9 | 10 | 11 | 12 | 1 |
| 历史(x分) | 79 | 81 | 83 | 85 | 87 |
| 政治(y分) | 77 | 79 | 79 | 82 | 83 |
分析 (1)利用所给数据,即可求该生5次月考历史成绩的平均分和政治成绩的方差;
(2)利用最小二乘法做出线性回归直线的方程的系数,写出回归直线的方程,得到结果.
解答 解:(1)$\overline{x}$=$\frac{1}{5}$(79+81+83+85+87)=83.
∵$\overline{y}$=$\frac{1}{5}$(77+79+79+82+83)=80,
∴政治成绩的方差=$\frac{1}{5}$[(77-80)2+(79-80)2+(79-80)2+(82-80)2+(83-80)2]=4.8
(2)$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)=30,$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=40,
∴b=$\frac{3}{4}$,
∴a=80-$\frac{3}{4}×83$=17.75,
∴y=$\frac{3}{4}$x+17.75.
点评 本题重点考查了线性回归直线方程及其求解,相关指数的计算等知识,属于中档题,考查运算求解能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
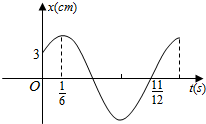 如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求:
如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com