
分析 (1)利用三角函数的奇偶性,求得φ的值,可得函数的解析式.
(2)利用余弦函数的周期性,可得f(x)的周期性,从而求得f(1)+f(2)+…+f(2017)的值.
(2)正弦函数的定义域和值域求得f(x)的值域,利用二次函数的性质,求得g(x)的最大值,再根据此最大值小于或等于$\sqrt{3}$m+3,求得m的范围.
解答 解:(1)∵偶函数f(x)=$cos(\frac{π}{ω}x-φ)$,其中ω>0,0≤φ<2π,∴φ=π.
(2)由(1)可得f(x)=-cos($\frac{π}{ω}$x ),函数f(x)在(0,3)上单调递减,
∴$\frac{π}{ω}•3$≤π,求得ω≥3,
故ω的最小值为3,此时,f(x)=-cos($\frac{π}{3}$x )的最小正周期为$\frac{2π}{\frac{π}{3}}$=6,
且f(1)+f(2)+…+f(6)=-$\frac{1}{2}$+($\frac{1}{2}$)+1+($\frac{1}{2}$)+(-$\frac{1}{2}$)+(-1)=0,
f(1)+f(2)+…+f(2017)=336•[f(1)+f(2)+…+f(6)]+f(2017)
=336•0+f(1)=-$\frac{1}{2}$.
(3)在(2)的条件下,$g(x)=-2{f^2}(x-\frac{3}{2})-f(x+\frac{3}{2})$=-2•${cos}^{2}[\frac{π}{3}(x-\frac{3}{2})]$+cos$\frac{π}{3}$(x+$\frac{3}{2}$)
=-2${sin}^{2}\frac{π}{3}x$-sin$\frac{π}{3}$x,
∵对任意的${x_1},{x_2}∈[-\frac{3}{2π},\frac{11}{2π}]$,∴$\frac{π}{3}$x1、$\frac{π}{3}$x2∈[-$\frac{1}{2}$,$\frac{11}{6}$],
∴sin$\frac{π}{3}$x∈[-sin$\frac{1}{2}$,1],故g(x)=-2${sin}^{2}\frac{π}{3}x$-sin$\frac{π}{3}$x=-2${(sin\frac{π}{3}x+\frac{1}{4})}^{2}$+$\frac{1}{8}$,
当sin$\frac{π}{3}$x=-$\frac{1}{4}$时,g(x)取得最大值为$\frac{1}{8}$,当sin$\frac{π}{3}$x=1时,g(x)取得最小值为-3.
再根据$8|g({x_1})-g({x_2})|≤\sqrt{3}m+3$恒成立,可得|g(x1)-g(x2)|的最大值为$\frac{1}{8}$+3=$\frac{25}{8}$,
故有8•$\frac{25}{8}$≤$\sqrt{3}$m+3,求得m≥$\frac{22\sqrt{3}}{3}$.
点评 本题主要考查三角函数的奇偶性和周期性,二次函数的性质,正弦函数的定义域和值域,函数的恒成立问题,属于中档题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
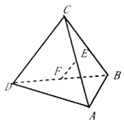 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )| A. | 120° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
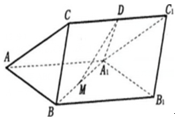 如图,三棱柱ABC-A1B1C1中,BC⊥平面ABB1A1,D,M分别为CC1和A1B的中点,△BA1B1是边长为2的正三角形,BC=1.
如图,三棱柱ABC-A1B1C1中,BC⊥平面ABB1A1,D,M分别为CC1和A1B的中点,△BA1B1是边长为2的正三角形,BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com