Question

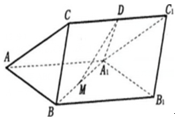
20．如图，三棱柱ABC-A₁B₁C₁中，BC⊥平面ABB₁A₁，D，M分别为CC₁和A₁B的中点，△BA₁B₁是边长为2的正三角形，BC=1．
（1）证明：MD∥平面ABC；
（2）求二面角A₁-AC-B的余弦值．

Answer 1

分析 （1）取AB的中点H，连接HM，CH，证明四边形CDMH是平行四边形得出DM∥CH，从而有DM∥平面ABC；
（2）取BB₁中点E，以E为原点建立坐标系，求出两半平面的法向量，计算法向量的夹角即可得出二面角的大小．

解答 （1）证明：取AB的中点H，连接HM，CH．
∵D，M分别为CC₁和A₁B的中点，
∴HM$\stackrel{∥}{=}$$\frac{1}{2}$AA₁，又CD$\stackrel{∥}{=}$$\frac{1}{2}$AA₁，
∴HM∥CD，HM=CD，
∴四边形CDMH是平行四边形，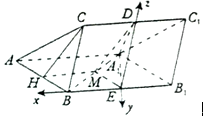
∴HC∥DM，又CH?平面ABC，DM?平面ABC，
∴MD∥平面ABC．
（2）解：取BB₁中点E，连结AE，
∵△A₁B₁E为等边三角形，
∴AE⊥BB₁，又BC⊥平面ABB₁A₁，DE∥BC，
∴DE⊥平面ABB₁A₁，
以E为坐标原点，分别以EB，A₁E，ED为x，y，z轴建立空间直角坐标系如图：
则$E（{0，0，0}），B（{1，0，0}），C（{1，0，1}），A（{2，-\sqrt{3}，0}），{A_1}（{0，-\sqrt{3}，0}）$，
则设平面ABC的法向量为$\overrightarrow n=（{x，y，z}）$，$\overrightarrow{AB}=（{-1，\sqrt{3}，0}），\overrightarrow{BC}=（{0，0，1}）$，则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{AB}=0\\ \overrightarrow n•\overrightarrow{BC}=0\end{array}\right.$，
即$\left\{\begin{array}{l}-x+\sqrt{3}y=0\\ z=0\end{array}\right.$，令y=1，则$x=\sqrt{3}，z=0$，即$\overrightarrow n=（{\sqrt{3}，1，0}）$，
平面ACA₁的法向量为$\overrightarrow m=（{x，y，z}）$，$\overrightarrow{AC}=（{-1，\sqrt{3}，0}），\overrightarrow{A{A_1}}=（{-2，0，0}）$，则$\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{AC}=0\\ \overrightarrow m•\overrightarrow{A{A_1}}=0\end{array}\right.$，
得$\left\{\begin{array}{l}-x+\sqrt{3}y+z=0\\-2x=0\end{array}\right.$，即$\left\{\begin{array}{l}x=0\\ z=-\sqrt{3}y\end{array}\right.$，令y=1，则$z=-\sqrt{3}，x=0$，即$\overrightarrow m=（{0，1，-\sqrt{3}}）$，
则$cos＜\overrightarrow m，\overrightarrow n＞=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}||{\overrightarrow n}|}}=\frac{1×1}{{\sqrt{{{（{\sqrt{3}}）}^2}+1•}\sqrt{{{（{-\sqrt{3}}）}^2}+1}}}=\frac{1}{2×2}=\frac{1}{4}$，
即二面角A₁-AC-B的余弦值是$\frac{1}{4}$．

点评 本题考查了线面平行的判定，空间向量与二面角的计算，属于中档题．