
分析 ①根据逆命题的定义结合方程根的关系进行判断.
②根据三角函数的周期公式以及充分条件和必要条件的定义进行判断.
③根据函数与方程的关系进行判断.
④根据幂函数的定义和性质进行判断.
⑤根据向量夹角和数量积的关系进行判断.
⑥构造函数,判断函数的单调性即可.
解答 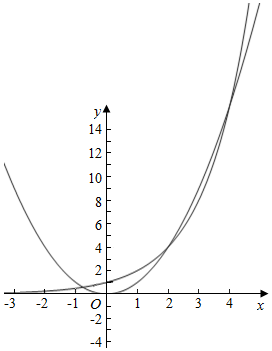 解:①命题“若方程ax2+x+1=0有两个实数根,则a≤$\frac{1}{4}$”的逆命题是若a≤$\frac{1}{4}$,则方程ax2+x+1=0有两个实数根,
解:①命题“若方程ax2+x+1=0有两个实数根,则a≤$\frac{1}{4}$”的逆命题是若a≤$\frac{1}{4}$,则方程ax2+x+1=0有两个实数根,
当a=0时,方程等价为x+1=0,则x=-1,此时方程只有一个根,故①错误;
②f(x)=cos2ax-sin2ax=cos2ax,
若“函数f(x)=cos2ax-sin2ax的最小正周期为π”,
则$\frac{2π}{2|a|}=π$,则|a|=1,则a=±1,
则充分性不成立,反之成立,
即“函数f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件正确,故②正确,
③由f(x)=2x-x2=0得2x=x2,
作出两个函数y=2x和y=x2的图象如图,由图象知两个函数交点个数为3个,故③错误;
④幂函数y=xa(a∈R)的图象恒过定点(0,0),错误,
当a<0时,函数的图象不过点(0,0),故④错误,
⑤“向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是钝角”的充分必要条件是“$\overrightarrow a$•$\overrightarrow b$<0”且$\overrightarrow a$≠λ$\overrightarrow b$,λ<0;故⑤错误,
⑥设f(x)=sinx-x,
则函数的导数f′(x)=cosx-1≤0,
则函数f(x)是奇函数,
∵f(0)=sin0-0=0,
∴f(x)=0的根只有一个0,解集方程sinx=x有一个实根.
故⑥错误,
故正确的是②,
故答案为:②
点评 本题主要考查命题的真假判断,涉及函数的性质,充分条件和必要条件的判断,涉及知识点较多,综合性较强,有一定 的难度.


科目:高中数学 来源: 题型:选择题
 我校为了了解高三学生在大庆市第一次模拟考试中对数学的掌握情况,从高三年级中随机抽查了100名学生的数学成绩,并制成了频率直方图,从图中可以知道这100名学生的平均分数和中位数分别为( )
我校为了了解高三学生在大庆市第一次模拟考试中对数学的掌握情况,从高三年级中随机抽查了100名学生的数学成绩,并制成了频率直方图,从图中可以知道这100名学生的平均分数和中位数分别为( )| A. | 103.2 113.2 | B. | 108.2 108 | C. | 103.2 108 | D. | 108.2 113.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com