
(本小题满分13分)
已知数列{an}的首项a1=" t" >0, ,n=1,2,……
,n=1,2,……
(1)若t = ,求
,求 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式;
(2)若 对一切
对一切 都成立,求t的取值范围.
都成立,求t的取值范围.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知曲线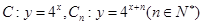 ,从
,从 上的点
上的点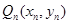 作
作 轴的垂线,交
轴的垂线,交 于点
于点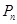 ,再从点
,再从点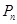 作
作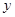 轴的垂线,交
轴的垂线,交 于点
于点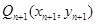 ,
,
设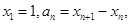
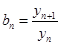 .。
.。 求数列
求数列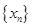 的通项公式;
的通项公式;  记
记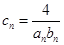 ,数列
,数列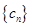 的前
的前 项和为
项和为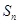 ,试比较
,试比较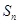 与
与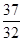 的大小
的大小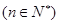 ;
;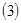 记
记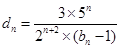 ,数列
,数列 的前
的前 项和为
项和为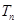 ,试证明:
,试证明: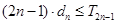 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知数列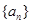 和
和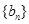 满足:
满足: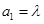 ,
,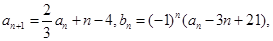 其中
其中 为实数,
为实数,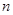 为正整数.
为正整数.
(1)对任意实数 ,证明数列
,证明数列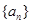 不是等比数列;
不是等比数列;
(2)试判断数列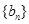 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(3)设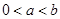 ,
,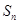 为数列
为数列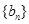 的前
的前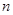 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数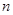 ,都有
,都有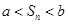 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com