
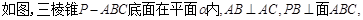
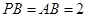 ,
,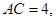
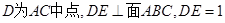 ,P、E在
,P、E在 同侧,连接PE、AE.
同侧,连接PE、AE.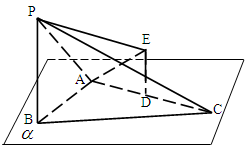
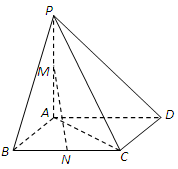
 求证:BC//面APE;
求证:BC//面APE; 设F是
设F是 内一点,且
内一点,且 ,求直线EF与面APF所成角的大小
,求直线EF与面APF所成角的大小 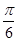 。
。 是解决的关键一步。
是解决的关键一步。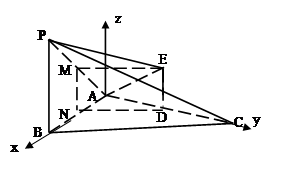
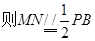 ,
,
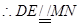 ,
,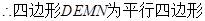 ,
,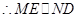 ,……..3分
,……..3分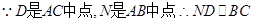 ,由公理4得
,由公理4得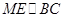 ,
,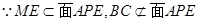
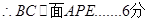
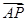 =(2,0,2),
=(2,0,2), =(0,2,1),设F(a,b,0),
=(0,2,1),设F(a,b,0),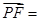 (a-2,b,-2),
(a-2,b,-2),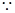 PF
PF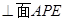 ,
,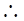
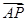
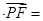 0,得a=4,同理
0,得a=4,同理
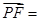 0,得b=1
0,得b=1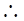 F(4,1,0),…… .9分
F(4,1,0),…… .9分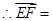 =(4,-1,-1),
=(4,-1,-1),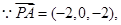
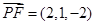
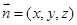 ,由
,由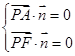 ,得
,得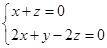 取一组解
取一组解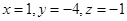 ,
,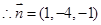 ,……11分
,……11分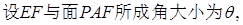
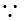 |cos
|cos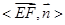 |=
|=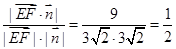 ,
, ,
,  ,直线EF与平面APF所成角大小为
,直线EF与平面APF所成角大小为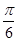 。……14分
。……14分

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
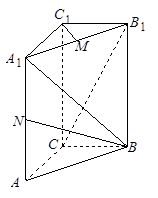
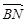 的长;
的长;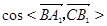 的值;
的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
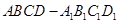 的棱
的棱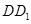 的中点,给出命题
的中点,给出命题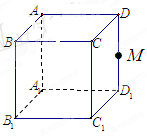
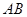 、
、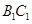 都相交;
都相交;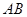 、
、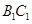 都垂直;
都垂直;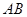 、
、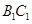 都相交;
都相交;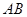 、
、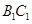 都平行.
都平行.| A.②③④ | B.①③④ | C.①②④ | D.①②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com