Question

【题目】已知关于与有表格中的数据，且与线性相关，由最小二乘法得.

	2	4	5	6	8
	30	40	60	50	70

（1）求与的线性回归方程；

（2）现有第二个线性模型：，且.若与（1）的线性模型比较，哪一个线性模型拟合效果比较好，请说明理由

Answer 1

【答案】(1) ＝6.5x＋17.5;(2) (1)的线性模型拟合效果比较好.

【解析】分析：(1)已知，可设线性回归方程为＝6.5x＋.要求方程，应利用样本点的中心在回归直线上，根据表中的数据可求得＝5，＝50. 代入方程可求得＝17.5.进而可得y与x的线性回归方程为＝6.5x＋17.5 . （2）要看哪一个线性模型拟合效果比较好，应求第一个模型的相关指数，由(1)的线性模型得yi－与yi－的关系如下表所示：

yi－	－0.5	－3.5	10	－6.5	0.5
yi－	－20	－10	10	0	20

由表中的数据和公式求得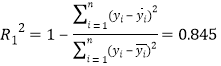。所以R＞R2。所以(1)的线性模型拟合效果比较好。

详解：(1)依题意设y与x的线性回归方程为＝6.5x＋.

由表中的数据可得 ，

因为直线＝6.5x＋经过(，)，

所以50＝6.5×5＋。

所以＝17.5.

所以y与x的线性回归方程为＝6.5x＋17.5 .

(2)由(1)的线性模型得yi－与yi－的关系如下表所示：

yi－	－0.5	－3.5	10	－6.5	0.5
yi－	－20	－10	10	0	20

所以 ，

所以=1- 。

由于R＝0.845，R2＝0.82

所以R＞R2，

所以(1)的线性模型拟合效果比较好．