
分析 根据题意,对于集合A={a1,a2,a3,…,a2016},将其中ai+aj的情况分行表示出来为,进而结合等差数列的性质分行分析其中重复的情况,进而结合L(A)的定义计算可得答案.
解答 解:根据题意,对于集合A={a1,a2,a3,…,a2016},将其中ai+aj的情况分行表示出来为:
a1+a2、a1+a3、a1+a4、a1+a5、…a1+a2016,
a2+a3、a2+a4、a2+a5、…a2+a2016,
a3+a4、a3+a5、…a3+a2016,
…
a2015+a2016,
其中第二行除了a2+a2016外,其余均与第一行有重复,即第二行只剩余一个不重复ai+aj的值,
同理,以下的2013行均只有一个一个不重复ai+aj的值,
则L(A)=2015+1+…+1=2015+2014=4029;
故答案为:4029.
点评 本题考查等差数列的性质,涉及集合中元素的特征,关键是理解题干中L(A)的定义,其次要注意到集合中元素的互异性.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (22015+24031)2016 | B. | 22015+24031 | C. | 2016(22015+24031) | D. | 2016(22016+24032) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 不合格 |
| 男生(人) | 15 | x | 5 |
| 女生(人) | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2>k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?=2,φ=$\frac{π}{2}$ | B. | ?=2,φ=π | C. | ?=$\frac{1}{2}$,φ=$\frac{π}{2}$ | D. | ?=$\frac{1}{2}$,φ=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
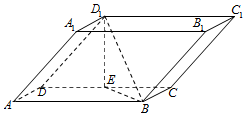 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com