
���� ����a��0ʱ������AΪ�����⣬������AΪ�����⣬����a��0�����ü��θ�����ø��ʣ�
�����ȵó����п��ܵ����ԣ��ٸ��ݺ����õ����Եõ�����Ҫʹ�¼�B������ֻ��f��1����g��1���̶��ó����ۣ�
��� �⣺����a��0ʱ������AΪ�����⣬������AΪ�����⣬����a��0��
��-1��a��3���ɼ��θ���֪ʶ�ɵ�����AΪ������ĸ���ΪP��A��=$\frac{2}{3}$
�������п��ܵ����ԣ�a��b��Ϊ��-1��-2����-1��-1������-1��1������-1��2������0��-2����0��-1����
��0��1������0��2������1��-2������1��-1������1��1������1��2������2��-2������2��-1������2��1������2��2��������16����
��Ϊx��1ʱ���գ�x��=g��x��=b+lnx�����䣨1��+�ޣ�������������
����?x1��x2��[1��+�ޣ���x1��x2��$\frac{�գ�{x}_{1}��-�գ�{x}_{2}��}{{x}_{1}-{x}_{2}}��0$����������Ҫʹ�¼�B������ֻ��f��1����g��1��
��a+b��0���������������ԣ�a��b��Ϊ��-1��-2����-1��-1������-1��1����������0��-2����0��-1������1��-2������1��-1������2��-2������8����
�����ɹŵ����֪ʶ�ɵ�P��B��=$\frac{8}{16}=\frac{1}{2}$��
���� ������Ҫ����ŵ���ͺͼ��θ��ͣ��������ͣ��߿�ʱ�п��飮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
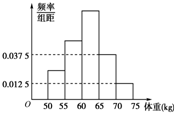 Ϊ���˽�ij�ؽ���߿�����������רҵ��ѧ������������������õ�ѧ���������ݷ�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3С���Ƶ��a��b��cǡ�ɵȲ����У�����ȡ��ѧ��������48�����2С���Ƶ��Ϊ��������
Ϊ���˽�ij�ؽ���߿�����������רҵ��ѧ������������������õ�ѧ���������ݷ�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3С���Ƶ��a��b��cǡ�ɵȲ����У�����ȡ��ѧ��������48�����2С���Ƶ��Ϊ��������| A�� | 6 | B�� | 12 | C�� | 18 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}[{1-{{��{\frac{1}{3}}��}^5}}]$ | B�� | $\frac{1}{3}[{1-{{��{\frac{1}{3}}��}^5}}]$ | C�� | $\frac{2}{3}[{1-{{��{\frac{1}{2}}��}^5}}]$ | D�� | $\frac{3}{2}[{1-{{��{\frac{1}{2}}��}^5}}]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | ||
| C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com