【题目】在扶贫活动中，为了尽快脱贫（无债务）致富，企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙，并约定从该店经营的利润中，首先保证企业乙的全体职工每月最低生活费的开支3 600元后，逐步偿还转让费（不计息）.在甲提供的资料中：①这种消费品的进价为每件14元；②该店月销量Q（百件）与销售价格P（元）的关系如图所示；③每月需各种开支2 000元.

（1）当商品的价格为每件多少元时，月利润扣除职工最低生活费的余额最大？并求最大余额；

（2）企业乙只依靠该店，最早可望在几年后脱贫？

参考答案：

【答案】(1) 19.5元，450元；（2）20年.

【解析】试题分析：（1）根据利润等于销售额乘以单价减去成本得：L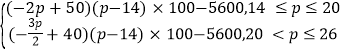＝，再分段根据二次函数对称轴与定义区间位置关系求最大值，最后取两个最大值中最大值（2） 由脱贫的含义：无债务，列不等式：12n×450－50 000－58 000≥0，解得n≥20.

试题解析：设该店月利润余额为L元，

则由题设得L＝Q（P－14）×100－3 600－2 000，（*）

由销量图易得Q＝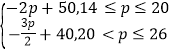

代入*式得L＝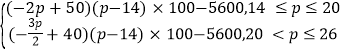

（1）当14≤P≤20时，Lmax＝450元，此时P＝19.5元；

当20＜P≤26时，Lmax＝元，此时P＝元.

故当P＝19.5元时，月利润余额最大，为450元.

（2）设可在n年后脱贫，

依题意有12n×450－50 000－58 000≥0，解得n≥20.

即最早可望在20年后脱贫.

关闭