
科目:高中数学 来源: 题型:选择题
| A. | (-1,3] | B. | [-3,1] | C. | [-1,2) | D. | [-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 图形的对称,正弦曲线的流畅都能体现“数学美”.“黄金分割”也是数学美得 一种体现,如图,椭圆的中心在原点,F为左焦点,当$\overrightarrow{FB}⊥\overrightarrow{AB}$时,其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{\sqrt{5}+1}{2}$.
图形的对称,正弦曲线的流畅都能体现“数学美”.“黄金分割”也是数学美得 一种体现,如图,椭圆的中心在原点,F为左焦点,当$\overrightarrow{FB}⊥\overrightarrow{AB}$时,其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{\sqrt{5}+1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=2\sqrt{2}x+1$ | B. | $y=\sqrt{3}x+1$ | C. | $y=\sqrt{2}x+1$ | D. | $y=2\sqrt{3}x+2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
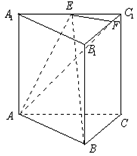 已知直三棱柱ABC-A1B1C1的底面为正三角形,E,F分别是A1C1,B1C1上的点,且满足A1E=EC1,B1F=3FC1.
已知直三棱柱ABC-A1B1C1的底面为正三角形,E,F分别是A1C1,B1C1上的点,且满足A1E=EC1,B1F=3FC1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=xsinx+3 | B. | y=x3 | C. | y=-sinx | D. | y=-3x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-1 | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com