
【题目】已知![]()
(1)求![]() ;
;
(2)我们知道二项式![]() 的展开式
的展开式![]() ,若等式两边对
,若等式两边对![]() 求导得
求导得![]() ,令
,令![]() 得
得![]() .利用此方法解答下列问题:
.利用此方法解答下列问题:
①求![]() ;
;
②求![]() .
.
【答案】(1)1;(2)①2n;②4n2-2n.
【解析】
(1)采用赋值法,令![]() ,求系数的和;(2)①原式
,求系数的和;(2)①原式![]() 两边求导,得
两边求导,得![]() ,再赋值
,再赋值![]() 求值;②
求值;②![]() 两边同时乘以
两边同时乘以![]() ,然后两边再求导,赋值
,然后两边再求导,赋值![]() 求值.
求值.
(1) 对于(2x-1)n=a0+a1x+a2x2+…+anxn,
取x=1得a0+a1+a2+…+an=1.
(2) ①对(2x-1)n=a0+a1x+a2x2+…+anxn两边求导得2n(2x-1)n-1=a1+2a2x+3a3x2+…+nanxn-1,
取x=1得a1+2a2+3a3+…+nan=2n.
②将2n(2x-1)n-1=a1+2a2x+3a3x2+…+nanxn-1两边乘以x得
2n(2x-1)n-1·x=a1x+2a2x2+3a3x3+…+nanxn,
两边求导得
2n[2(n-1)(2x-1)n-2x+(2x-1)n-1]=a1+22a2x+32a3x2+…+n2anxn-1,
取x=1得12a1+22a2+32a3+…+n2an=4n2-2n.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图象如图所示,则下列叙述正确的是( )
的部分图象如图所示,则下列叙述正确的是( )
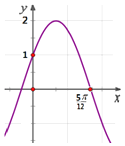
A.函数![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位得到
个单位得到
B.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C.函数![]() 在区间
在区间![]() 上是单调递增的
上是单调递增的
D.函数![]() 图象的对称中心为
图象的对称中心为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年,“非典”爆发,以钟南山为代表的医护工作者经长期努力,抗击了非典.
年,“非典”爆发,以钟南山为代表的医护工作者经长期努力,抗击了非典.![]() 年
年![]() 岁高龄的钟院士再次披挂上阵,逆行武汉抗击新冠疫情。为调查中学生对这一伟大“逆行者”的了解程度,某调查小组随机抽取了某市物化生、政史地的
岁高龄的钟院士再次披挂上阵,逆行武汉抗击新冠疫情。为调查中学生对这一伟大“逆行者”的了解程度,某调查小组随机抽取了某市物化生、政史地的![]() 名高中生,请他们列举钟南山院士在医学上的成就,把能列举钟南山成就不少于
名高中生,请他们列举钟南山院士在医学上的成就,把能列举钟南山成就不少于![]() 项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:
项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:
组合 | 0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 |
物化生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
政史地(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)请将下面的2×2列联表补充完整;
组合 | 比较了解 | 不太了解 | 合计 |
物化生 | |||
政史地 | |||
合计 |
(2)判断是否有99%的把握认为,了解钟南山与选择物化生、政史地组合有关?
参考:![]()
![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
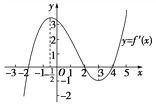
①函数y=f(x)在区间![]() 内单调递增;
内单调递增;
②函数y=f(x)在区间![]() 内单调递减;
内单调递减;
③函数y=f(x)在区间(4,5)内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x=![]() 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
则上述判断中正确的是( )
A. ①② B. ②③
C. ③④⑤ D. ③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级三个班共有学生120名,这三个班的男女生人数如下表所示,已知在全年级中随机抽取1名学生,抽到二班女生的概率是0.2,则![]() _________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
_________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
一班 | 二班 | 三班 | |
女生人数 | 20 |
|
|
男生人数 | 20 | 20 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 、
、![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com