
【题目】已知函数![]() .(
.(![]() 是自然对数的底数)
是自然对数的底数)
(1)求![]() 的单调递减区间;
的单调递减区间;
(2)若函数![]() ,证明
,证明![]() 在
在![]() 上只有两个零点.(参考数据:
上只有两个零点.(参考数据:![]() )
)
【答案】(1)![]() (k∈Z).(2)见解析.
(k∈Z).(2)见解析.
【解析】
(1)由f'(x)<0得![]() ,利用正弦函数的单调性质可得f(x)的单调递减区间;
,利用正弦函数的单调性质可得f(x)的单调递减区间;
(2)依题意可得g'(x)=ex(sinx+cosx)﹣2,分析其单调情况并作出图象,利用零点存在性定理可得,g(x)在(x1,x2)和(x2,π)内各有一个零点,从而可证得结论成立.
(1)f(x)=exsinx,定义域为R.![]() .
.
由f'(x)<0得![]() ,解得
,解得![]() (k∈Z).
(k∈Z).
∴f(x)的单调递减区间为![]() (k∈Z).
(k∈Z).
(2)∵g'(x)=ex(sinx+cosx)﹣2,∴g'(x)=2excosx.
∵x∈(0,π),∴当![]() 时,g'(x)>0;当
时,g'(x)>0;当![]() 时,g'(x)<0.
时,g'(x)<0.
∴g'(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
又∵g'(0)=1﹣2<0,![]() ,g'(π)=﹣eπ﹣2<0,
,g'(π)=﹣eπ﹣2<0,
∴g'(x)在(0,π)上图象大致如右图.
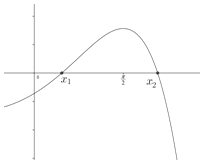
∴![]() ,
,![]() ,使得g'(x1)=0,g'(x2)=0,
,使得g'(x1)=0,g'(x2)=0,
且当x∈(0,x1)或x∈(x2,π)时,g'(x)<0;当x∈(x1,x2)时,g'(x)>0.
∴g(x)在(0,x1)和(x2,π)上单调递减,在(x1,x2)上单调递增.
∵g(0)=0,∴g(x1)<0.
∵![]() ,∴g(x2)>0,
,∴g(x2)>0,
又∵g(π)=﹣2π<0,由零点存在性定理得,g(x)在(x1,x2)和(x2,π)内各有一个零点,
∴函数g(x)在(0,π)上有两个零点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求家庭的月储蓄![]() 对月收入
对月收入![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
(附:线性回归方程![]() 中,
中,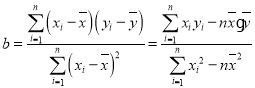 ,其中
,其中![]() ,
,![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=log2(kx2+4kx+3).①若f(x)的定义域为R,则k的取值范围是_____;②若f(x)的值域为R,则k的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
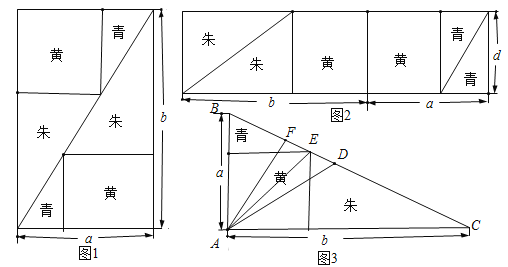
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得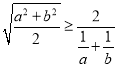 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则下列结论正确的是( )
A.四面体ABCD每组对棱相互垂直
B.四面体ABCD每个面的面积相等
C.从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°且小于180°
D.连接四面体ABCD每组对棱中点的线段相互垂直平分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于![]() 的说法,正确的是( )
的说法,正确的是( )
A.展开式中的二项式系数之和为2048
B.展开式中只有第6项的二项式系数最大
C.展开式中第6项和第7项的二项式系数最大
D.展开式中第6项的系数最小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数![]() 的图象,只要将函数
的图象,只要将函数![]() 的图象( )
的图象( )
A.每一点的横坐标变为原来的![]() 倍(纵坐标不变),再将所得图象向左平移
倍(纵坐标不变),再将所得图象向左平移![]() 个长度
个长度
B.每一点的横坐标变为原来的![]() 倍(纵坐标不变),再将所得图象向左平移
倍(纵坐标不变),再将所得图象向左平移![]() 个长度
个长度
C.向左平移![]() 个长度,再将所得图象每一点的横坐标变为原来的
个长度,再将所得图象每一点的横坐标变为原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
D.向左平移![]() 个长度,再将所得图象每一点的横坐标变为原来的
个长度,再将所得图象每一点的横坐标变为原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com