
分析 (1)由分母不为0,结合余弦函数的图象可得定义域;
(2)运用两角差的余弦公式和二倍角公式,化简整理可得f(x)=2$\sqrt{2}$sin(x+$\frac{π}{4}$),由x的范围,可得x+$\frac{π}{4}$的范围,运用正弦函数的图象和性质,可得最值.
解答 解:(1)函数f(x)=$\frac{1+\sqrt{2}cos(2x-\frac{π}{4})}{cosx}$,
可得cosx≠0,即x≠kπ+$\frac{π}{2}$,k∈Z,
即有函数f(x)的定义域为{x|x≠kπ+$\frac{π}{2}$,k∈Z};
(2)f(x)=$\frac{1+\sqrt{2}cos(2x-\frac{π}{4})}{cosx}$=$\frac{1+\sqrt{2}(cos2xcos\frac{π}{4}+sin2xsin\frac{π}{4})}{cosx}$=$\frac{1+cos2x+sin2x}{cosx}$=$\frac{2co{s}^{2}x+2sinxcosx}{cosx}$
=2(sinx+cosx)=2$\sqrt{2}$sin(x+$\frac{π}{4}$),
当x∈[-$\frac{π}{4}$,$\frac{π}{2}$),可得x+$\frac{π}{4}$∈[0,$\frac{3π}{4}$),
当x+$\frac{π}{4}$=$\frac{π}{2}$,即x=$\frac{π}{4}$时,f(x)取得最大值2$\sqrt{2}$;
当x+$\frac{π}{4}$=0,即x=-$\frac{π}{4}$时,f(x)取得最小值2.
点评 本题考查三角函数的化简和求值,注意运用两角差的余弦公式和二倍角公式,正弦函数的图象和性质,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
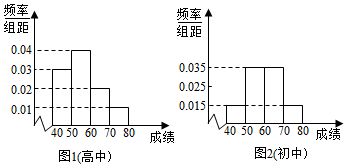
| 成绩小于60分的人数 | 成绩不小于60分人数 | 合计 | |
| 初中年级 | |||
| 高中年级 | |||
| 合计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
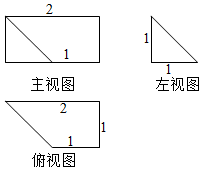
| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
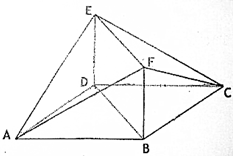 如图,多面ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°,四边形BDEF是正方形.
如图,多面ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°,四边形BDEF是正方形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
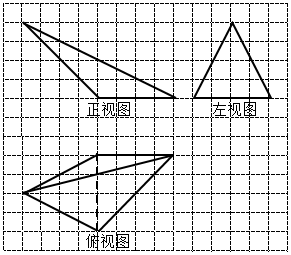 如图,网格纸上每个小正方形的边长均为1,某几何体的三视图如图中粗线所示,则该几何体的所有棱中最长的棱的长度是( )
如图,网格纸上每个小正方形的边长均为1,某几何体的三视图如图中粗线所示,则该几何体的所有棱中最长的棱的长度是( )| A. | 4$\sqrt{6}$ | B. | 2$\sqrt{21}$ | C. | 6 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com