
| 成绩小于60分的人数 | 成绩不小于60分人数 | 合计 | |
| 初中年级 | |||
| 高中年级 | |||
| 合计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
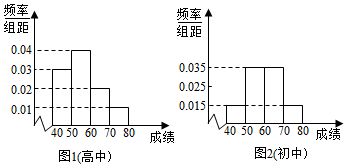
分析 (1)初中年级成绩在[70,80)之间的学生共有0.015×10×40=6人,恰有4名女同学,2名男同学,利用对立事件的概率公式,即可求其中至少有1名男同学的概率;
(2)根据列联表中的数据,计算K2的值,即可得到结论.
解答 解:(1)初中年级成绩在[70,80)之间的学生共有0.015×10×100=15人,恰有5名女同学,10名男同学,
现从成绩在该组的初中年级的学生任选2名同学,有C152=105种情况,全是男同学有C102=45种情况
∴其中至少有1名女同学的概率为1-$\frac{45}{105}$=$\frac{4}{7}$;
(2)2×2列联表
| 成绩小于60分的人数 | 成绩不小于60分人数 | 合计 | |
| 初中年级 | 50 | 50 | 100 |
| 高中年级 | 70 | 30 | 100 |
| 合计 | 120 | 80 | 200 |
点评 本题考查独立性检验,考查概率的计算,考查学生的阅读与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{21}-12}}{5}$ | B. | $\frac{{12-\sqrt{21}}}{5}$ | C. | $\frac{{2\sqrt{21}-12}}{5}$ | D. | $\frac{{12-2\sqrt{21}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
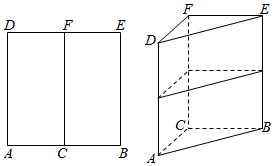
 如图,四棱锥B-ADEF中,平面ABD⊥平面ADEF,其中AB⊥AD,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1.
如图,四棱锥B-ADEF中,平面ABD⊥平面ADEF,其中AB⊥AD,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=3,BE=$\frac{1}{2}$EC,AD=2DC,AE=$\sqrt{2}$.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=3,BE=$\frac{1}{2}$EC,AD=2DC,AE=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 32π | C. | 8π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 工作 效益 机器 | 一 | 二 | 三 | 四 | 五 |
| 甲 | 15 | 17 | 14 | 17 | 15 |
| 乙 | 22 | 23 | 21 | 20 | 20 |
| 丙 | 9 | 13 | 14 | 12 | 10 |
| 丁 | 7 | 9 | 11 | 9 | 11 |
| 戊 | 13 | 15 | 14 | 15 | 11 |
| A. | 甲只能承担第四项工作 | B. | 乙不能承担第二项工作 | ||
| C. | 丙可以不承担第三项工作 | D. | 丁可以承担第三项工作 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
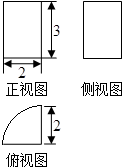
| A. | 3π+12 | B. | 5π | C. | 5π+12 | D. | 8π+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com