
分析 由题意,可得x1,x2为方程mx2-x+m=0的两个不同实数解,x1+x2=$\frac{1}{m}$,x1x2=1,表示出圆柱的体积,利用配方法,即可得出结论
解答 解:由题意,令y1=y2=m,x1,x2为方程mx2-x+m=0的两个不同实数解,
∴x1+x2=$\frac{1}{m}$,x1x2=1,
矩形绕x轴旋转一周得到的圆柱的体积V=πm2|x1-x2|=πm2•$\sqrt{\frac{1}{{m}^{2}}-4}$=π$\sqrt{-4({m}^{2}-\frac{1}{8})^{2}+\frac{1}{16}}$,
∴m2=$\frac{1}{8}$时,矩形绕x轴旋转一周得到的圆柱的体积的最大值为$\frac{π}{4}$,
故答案为:$\frac{π}{4}$.
点评 本题考查旋转体的体积,考查韦达定理的运用,正确表示圆柱的体积是关键.


科目:高中数学 来源: 题型:解答题
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为BB1,CD的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为BB1,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体EF-ABCD中,ABCD,ABEF均为直角梯形,$∠ABE=∠ABC=\frac{π}{2}$,DCEF为平行四边形,平面DCEF⊥平面ABCD.
如图,在多面体EF-ABCD中,ABCD,ABEF均为直角梯形,$∠ABE=∠ABC=\frac{π}{2}$,DCEF为平行四边形,平面DCEF⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
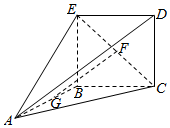 如图所示,正方形BCDE所在的平面与平面ABC互相垂直,其中∠ABC=120°,AB=BC=2,F,G分别为CE,AB的中点.
如图所示,正方形BCDE所在的平面与平面ABC互相垂直,其中∠ABC=120°,AB=BC=2,F,G分别为CE,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
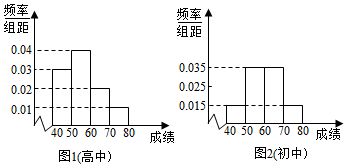
| 成绩小于60分的人数 | 成绩不小于60分人数 | 合计 | |
| 初中年级 | |||
| 高中年级 | |||
| 合计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月收入 | [15,25) | [25,35) | [35,45) | [45,45) | [55,65) | [65,75) |
| 频数 | 10 | 20 | 30 | 20 | 10 | 10 |
| 赞成人数 | 8 | 16 | 24 | 12 | 6 | 4 |
| 月收入低于55百元的人数 | 月收入高于55百元的人数 | 合计 | |
| 赞成 | a= | c= | |
| 不赞成 | b= | d= | |
| 合计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 没有同时报考“华约”和“卓越”联盟的考生 | |
| B. | 报考“华约”和“京派”联盟的考生一样多 | |
| C. | 报考“北约”联盟的考生也报考了“卓越”联盟 | |
| D. | 报考“京派”联盟的考生也报考了“北约”联盟 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
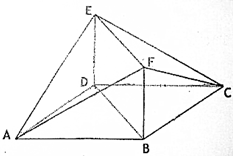 如图,多面ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°,四边形BDEF是正方形.
如图,多面ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°,四边形BDEF是正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com