
| A. | $\frac{{\sqrt{21}-12}}{5}$ | B. | $\frac{{12-\sqrt{21}}}{5}$ | C. | $\frac{{2\sqrt{21}-12}}{5}$ | D. | $\frac{{12-2\sqrt{21}}}{5}$ |
分析 设P(2cosθ,$\sqrt{3}$sinθ),0≤θ<2π,运用点到直线的距离公式和辅助角公式,及正弦函数的值域加上即可得到所求最小值.
解答 解:P是椭圆C:$\frac{x^2}{4}+\frac{y^2}{3}$=1上的动点,
可设P(2cosθ,$\sqrt{3}$sinθ),0≤θ<2π,
P到直线$\frac{x}{4}+\frac{y}{3}$=1即3x+4y-12=0的距离为d=$\frac{|6cosθ+4\sqrt{3}sinθ-12|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{1}{5}$|$\sqrt{36+48}sin(θ+α)$-12|
=$\frac{1}{5}$|2$\sqrt{21}$sin(θ+α)-12|,α为辅助角.
当sin(θ+α)=1时,P到直线$\frac{x}{4}+\frac{y}{3}$=1的距离的最小值为$\frac{12-2\sqrt{21}}{5}$.
故选:D.
点评 本题考查点到直线的距离的最值的求法,注意运用椭圆的参数方程和辅助角公式,考查正弦函数的值域,属于中档题.


科目:高中数学 来源: 题型:选择题
| 男 | 女 | 合 计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 合 计 | 60 | 50 | 110 |
| A. | 有99%的把握认为“爱好该项运动与性别有关” | |
| B. | 有99%的把握认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (sinx)′=-cosx | B. | (cosx)′=sinx | C. | (2x)′=x•2x-1 | D. | ($\frac{1}{x}$)′=-$\frac{1}{{x}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
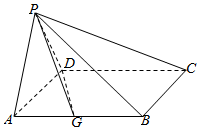 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
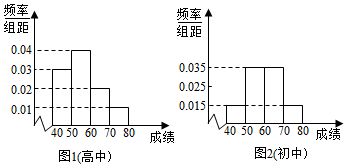
| 成绩小于60分的人数 | 成绩不小于60分人数 | 合计 | |
| 初中年级 | |||
| 高中年级 | |||
| 合计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com