Question

13．已知函数$f（x）=\left\{\begin{array}{l}{3^{|x-1|}}，x＞0\\-{x^2}-2x+1，x≤0\end{array}\right.$，若关于x的方程f²（x）+（a-1）f（x）-a=0有7个不等的实数根，则实数a的取值范围是（　　）

• A． [1，2]
• B． （1，2）
• C． （-2，-1）
• D． [-2，-1]

Answer 1

分析 画出函数的图象，利用函数的图象，判断f（x）的范围，然后利用二次函数的性质求解a的范围．

解答 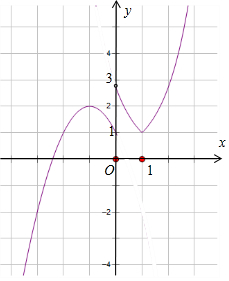解：函数$f（x）=\left\{\begin{array}{l}{3^{|x-1|}}，x＞0\\-{x^2}-2x+1，x≤0\end{array}\right.$的图象如图：
关于f²（x）+（a-1）f（x）-a=0有7个不等的实数根，
即[f（x）+a][f（x）-1]=0有7个不等的实数根，f（x）=1有3个不等的实数根，
∴f（x）=-a必须有4个不相等的实数根，由函数f（x）图象
可知-a∈（1，2），∴a∈（-2，-1）．
故选：C．

点评 本题考查函数与方程的应用，函数的零点个数的判断与应用，考查数形结合以及计算能力．