
���� �������ü�������ֱ�����껥��������������C��ֱ�����귽�̣�
����$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\sqrt{3}+\sqrt{3}t\end{array}\right.$������$y-\sqrt{3}{x^2}=0$�ã�$\sqrt{3}+\sqrt{3}t-\sqrt{3}{��{1+\frac{1}{2}t}��^2}=0$������������꣬����ֱ��l������C�����һ�������꣮
��� �⣺����$sin��-\sqrt{3}��{cos^2}��=0$����$��sin��-\sqrt{3}{��^2}{cos^2}��=0$��
��$y-\sqrt{3}{x^2}=0$��
����$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\sqrt{3}+\sqrt{3}t\end{array}\right.$������$y-\sqrt{3}{x^2}=0$�ã�$\sqrt{3}+\sqrt{3}t-\sqrt{3}{��{1+\frac{1}{2}t}��^2}=0$����t=0��
�Ӷ�����������Ϊ$��{1��\sqrt{3}}��$��
���ԣ������һ��������Ϊ$��{2��\frac{��}{3}}��$��
���� ���⿼�鼫������ֱ�����껥��������������̵����ã��Ƚϻ�����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �ؾ������ҹ�����ʱ�ڵ���ѧ�ң����ݣ����Ĵ�ʡ�����أ��ˣ����������ġ�������¡�������Ķ���ʽ��ֵ���ؾ����㷨���������DZȽ��Ƚ����㷨����ͼ��ʾ�ij����ͼ�����������ؾ����㷨��ij����ʽֵ��һ��ʵ����������x��ֵΪ2�������v��ֵΪ��������
�ؾ������ҹ�����ʱ�ڵ���ѧ�ң����ݣ����Ĵ�ʡ�����أ��ˣ����������ġ�������¡�������Ķ���ʽ��ֵ���ؾ����㷨���������DZȽ��Ƚ����㷨����ͼ��ʾ�ij����ͼ�����������ؾ����㷨��ij����ʽֵ��һ��ʵ����������x��ֵΪ2�������v��ֵΪ��������| A�� | 210-1 | B�� | 210 | C�� | 310-1 | D�� | 310 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-2���ȣ�2��+�ޣ� | B�� | ��-2��0���ȣ�0��2�� | C�� | {x|x�١�2} | D�� | ��-2��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
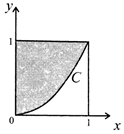 ����ͼ��ʾ�������������Ͷ��10000���㣬��������Ӱ���֣�����C�ķ���Ϊx2-y=0���ĵ�ĸ����Ĺ���ֵΪ��������
����ͼ��ʾ�������������Ͷ��10000���㣬��������Ӱ���֣�����C�ķ���Ϊx2-y=0���ĵ�ĸ����Ĺ���ֵΪ��������| A�� | 5000 | B�� | 6667 | C�� | 7500 | D�� | 7854 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��1.5�� | B�� | ��1.5��2�� | C�� | ��2��2.5�� | D�� | ��2.5��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��2] | B�� | ��1��2�� | C�� | ��-2��-1�� | D�� | [-2��-1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��-1��$\frac{3}{2}$} | B�� | {-2��1��-$\frac{3}{2}$��-1} | C�� | {1} | D�� | {2��1��-1��$\frac{3}{2}$} |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com