
分析 (I)利用等差数列的求和公式及其通项公式即可得出.
(II)通过分类讨论,利用等差数列与等比数列的求和公式即可得出.
解答 解:(Ⅰ)因为{an}为等差数列,
所以$\left\{\begin{array}{l}{S_4}=4{a_1}+\frac{4×3}{2}d=24\\{S_7}=7{a_1}+\frac{7×6}{2}d=63\end{array}\right.⇒\left\{\begin{array}{l}{a_1}=3\\ d=2\end{array}\right.⇒{a_n}=2n+1$.
(Ⅱ)∵${b_n}={2^{a_n}}+{({-1})^n}•{a_n}={2^{2n+1}}+{({-1})^n}•({2n+1})=2×{4^n}+{({-1})^n}•({2n+1})$
∴${T_n}=2({{4^1}+{4^2}+…+{4^n}})+[{-3+5-7+9-…+{{({-1})}^n}({2n+1})}]=\frac{{8({{4^n}-1})}}{3}+{G_n}$,
当n=2k(k∈N*)时,${G_n}=2×\frac{n}{2}=n$,∴${T_n}=\frac{{8({{4^n}-1})}}{3}+n$
当n=2k-1(k∈N*)时,${G_n}=2×\frac{n-1}{2}-({2n+1})=-n-2$,
∴${T_n}=\frac{{8({{4^n}-1})}}{3}-n-2$,∴${T_n}=\left\{\begin{array}{l}\frac{{8({{4^n}-1})}}{3}+n({n=2k,k∈{N^*}})\\ \frac{{8({{4^n}-1})}}{3}-n-2({n=2k-1,k∈{N^*}})\end{array}\right.$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{64},1]$ | B. | $[\frac{1}{8},1]$ | C. | $(\frac{1}{64},1)$ | D. | $(\frac{1}{8},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
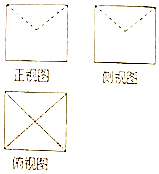 某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件 | |
| B. | 已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有$\frac{1}{{x}^{2}}$<$\frac{1}{{x}^{3}}$,则p∧(¬q)是真命题 | |
| C. | 命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0” | |
| D. | 从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是分成抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
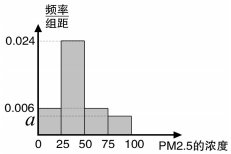 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:| 组别 | PM2.5浓度 (微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 3 | 0.15 |
| 第二组 | (25,50] | 12 | 0.6 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com