Question

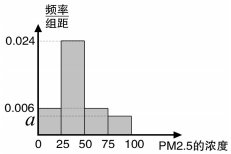
6．根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2.5的年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米．我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度（单位：微克/立方米）的监测数据，数据统计如表：

组别	PM2.5浓度 （微克/立方米）	频数（天）	频率
第一组	（0，25]	3	0.15
第二组	（25，50]	12	0.6
第三组	（50，75]	3	0.15
第四组	（75，100]	2	0.1

（1）将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图．
①求图4中a的值；
②求样本平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境质量是否需要改善？并说明理由．
（2）将频率视为概率，对于2016年的某3天，记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X，求X的分布列和数学期望．

Answer 1

分析 （1）①a=0.004．②2016年该居民区PM2.5的年平均浓度=12.5×0.15+37.5×0.6+62.5×0.15+87.5×0.1，与35比较即可判断出结论．
（2）由题意可得：PM2.5的24小时平均浓度符合环境空气质量标准的概率为0.9，X的可能取值为0，1，2，3．P（X=k）=${∁}_{3}^{k}（0.1）^{3-k}（0.9）^{k}$．

解答 解：（1）①a=0.004．②2016年该居民区PM2.5的年平均浓度=12.5×0.15+37.5×0.6+62.5×0.15+87.5×0.1=42.5（微克/立方米），∵42.5＞35，∴2016年该居民区PM2.5的年平均浓度不符合环境空气质量标准，故该居民取的环境需要改进．
（2）由题意可得：PM2.5的24小时平均浓度符合环境空气质量标准的概率为0.9，X的可能取值为0，1，2，3．P（X=k）=${∁}_{3}^{k}（0.1）^{3-k}（0.9）^{k}$，可得P（X=0）=0.001，P（X=1）=0.027，P（X=2）=0.243，
P（X=3）=0.729．
X的分布列为：

X	0	1	2	3
P	0.001	0.027	0.243	0.729

E（X）=0×0.001+1×0.027+2×0.243+3×0.729=2.7，或E（X）=3×0.9=2.7．

点评 本题考查了频率分布直方图的性质及其应用、二项分布列的概率计算公式及其数学期望，考查推理能力与计算能力，属于中档题．