
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
分析 由已知中S、A、B、C是球O表面上的点,SA⊥平面ABC,AB⊥BC,易S、A、B、C四点均为长宽高分别SA,AB,BC三边长的长方体的顶点,由长方体外接球的直径等于长方体对角线,利用球的表面积公式即可得到答案.
解答 解:∵SA⊥平面ABC,AB⊥BC,
∴四面体S-ABC的外接球半径等于以长宽高分别SA,AB,BC三边长的长方体的外接球的半径
∵球O的表面积为4π,∴R=1
∵AB=1,BC=$\sqrt{2}$,
∴2R=$\sqrt{1+2+S{A}^{2}}$=2,
∴SA=1
故选B.
点评 本题考查的知识点是球内接多面体,球的表面积公式,其中根据已知条件求出球O的直径(半径),是解答本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
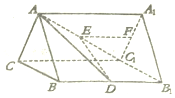 在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C为矩形,D,E,F分别是线段BB1,AC1,A1C1的中点.
在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C为矩形,D,E,F分别是线段BB1,AC1,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
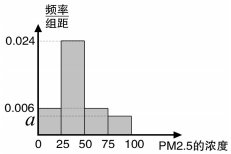 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:| 组别 | PM2.5浓度 (微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 3 | 0.15 |
| 第二组 | (25,50] | 12 | 0.6 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{8}$ | D. | -$\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不等边锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1,1 | B. | -$\frac{3}{2}$,-1 | C. | -$\frac{3}{2}$,3 | D. | -2,$\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com