已知集合A={-2.0.2}.B={x|2x2-2x-3≤1}.则A∩B=( )A．{0}B．{2}C．{0.2}D．{-2.0} 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

14．已知集合A={-2，0，2}，B={x|2^x²-2x-3≤1}，则A∩B=（　　）

A．

{0}

B．

{2}

C．

{0，2}

D．

{-2，0}

分析先分别求出集合A和B，由此利用交集性质能求出A∩B．

解答解：∵集合A={-2，0，2}，
B={x|2^x²-2x-3≤1}={x|-1＜x＜3}，
∴A∩B={0，2}．
故选：C．

点评本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

4．数列{a_n}的前n项和为S_n，S_n=2a_n-n（n∈N^*）．
（1）求证：数列{a_n+1}成等比数列；
（2）求数列{a_n}的通项公式；
（3）数列{a_n}中是否存在连续三项可以构成等差数列？若存在，请求出一组适合条件的三项；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．下列说法正确的是（　　）

	A．	“sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件
	B．	已知命题p：?x∈R，使2^x＞3^x；命题q：?x∈（0，+∞），都有$\frac{1}{{x}^{2}}$＜$\frac{1}{{x}^{3}}$，则p∧（￢q）是真命题
	C．	命题“若xy=0，则x=0或y=0”的否命题是“若xy≠0，则x≠0或y≠0”
	D．	从匀速传递的生产流水线上，质检员每隔5分钟从中抽取一件产品进行某项指标检测，这是分成抽样

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．已知抛物线C：y²=8x的焦点为F，P为C的准线上一点，Q（在第一象限）是直线PF与C的一个交点，若$\overrightarrow{PQ}=\sqrt{2}\overrightarrow{QF}$，则QF的长为（　　）

A．

$6-4\sqrt{2}$

B．

$8-4\sqrt{2}$

C．

$8+4\sqrt{2}$

D．

$8±4\sqrt{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．

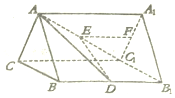在三棱柱ABC-A₁B₁C₁中，△ABC是边长为2的正三角形，侧面BB₁C₁C为矩形，D，E，F分别是线段BB₁，AC₁，A₁C₁的中点．
（1）求证：DE∥平面A₁B₁C₁；
（2）若平面ABC⊥平面BB₁C₁C，BB₁=4，求三棱锥C-AC₁D的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．在平面直角坐标系xoy中，双曲线${C_1}：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的渐近线与抛物线${C_2}：{y^2}=2px（{p＞0}）$交于点O，A，B，若△OAB的垂心为C₂的焦点，则C₁的离心率为（　　）

A．

$\frac{3}{2}$

B．

$\sqrt{5}$

C．

$\frac{{3\sqrt{5}}}{5}$

D．

$\frac{{\sqrt{5}}}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．

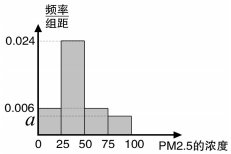根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2.5的年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米．我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度（单位：微克/立方米）的监测数据，数据统计如表：

组别	PM2.5浓度（微克/立方米）	频数（天）	频率
第一组	（0，25]	3	0.15
第二组	（25，50]	12	0.6
第三组	（50，75]	3	0.15
第四组	（75，100]	2	0.1

（1）将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图．
①求图4中a的值；
②求样本平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境质量是否需要改善？并说明理由．
（2）将频率视为概率，对于2016年的某3天，记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X，求X的分布列和数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

3．设函数f（x）=g（$\frac{x}{2}$）+x²，曲线y=g（x）在点（1，g（1））处的切线方程为9x+y-1=0，则曲线y=f（x）在点（2，f（2））处的切线方程为x+2y+6=0．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．曲线f（x）=$\frac{lnx}{x}$在x=e处的切线方程为（　　）

A．

y=e

B．

y=x-e+$\frac{1}{e}$

C．

y=x