
| A. | $\frac{3}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{3\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
分析 求出A的坐标,可得kAH=$\frac{4{b}^{2}}{4ab-{a}^{2}}$,利用△OAB的垂心为C2的焦点,可得$\frac{4{b}^{2}}{4ab-{a}^{2}}$×(-$\frac{b}{a}$)=-1,由此可求C1的离心率.
解答 解:双曲线${C_1}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的渐近线方程为y=±$\frac{b}{a}$x,
与抛物线C2:x2=2py联立,可得x=0或x=±$\frac{2pb}{a}$,
取A($\frac{2pb}{a}$,$\frac{2p{b}^{2}}{{a}^{2}}$),设垂心H($\frac{p}{2}$,0),
则kAH=$\frac{4{b}^{2}}{4ab-{a}^{2}}$,
∵△OAB的垂心为C2的焦点,
∴$\frac{4{b}^{2}}{4ab-{a}^{2}}$×(-$\frac{b}{a}$)=-1,
∴e=$\frac{c}{a}$=$\frac{3\sqrt{5}}{5}$.
故选C.
点评 本题考查双曲线的性质,考查学生的计算能力,确定A的坐标是关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:选择题
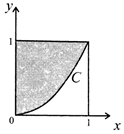 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )| A. | 5000 | B. | 6667 | C. | 7500 | D. | 7854 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,-1,$\frac{3}{2}$} | B. | {-2,1,-$\frac{3}{2}$,-1} | C. | {1} | D. | {2,1,-1,$\frac{3}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com