练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．若x0是方程lnx+x-3=0的实数解，则x0属于区间（　　）
    A．（1，1.5）B．（1.5，2）C．（2，2.5）D．（2.5，3）

    分析 由方程lnx+x=3，设对应函数f（x）=lnx+x-3，然后根据根的存在性定理进行判断即可．

    解答 解：∵方程lnx+x-3=0，
    ∴设对应函数f（x）=lnx+x-3，
    ∵f（2）=ln2+2-3=ln2-1＜0，f（2.5）=ln2.5+2.5-3=ln2.5-0.5lne＞0，
    ∴根据根的存在性定理可知在区间（2，2.5）内函数存在零点，
    即x0属于区间（2，2.5）．
    故选：C．

    点评 本题主要考查函数零点的判断，利用根的存在性定理是解决本题的关键，将方程转化为函数即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

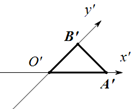    16．如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′，若O′B′=B′A′=1，那么原△ABO的面积是（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\sqrt{2}$D．2$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设p：x＜4，q：1＜x＜4，则p是q成立的（　　）
    A．充要条件B．充分不必要条件
    C．必要不充分条件D．既充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知$\vec a=（{1，3}）$，$\vec b=（{-2，k}）$，且$（{\vec a+2\vec b}）∥（{3\vec a-\vec b}）$，则实数k=-6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知直线l的参数方程为$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\sqrt{3}+\sqrt{3}t\end{array}\right.$（t为参数）以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C的方程为$sinθ-\sqrt{3}ρ{cos^2}θ=0$．
    （Ⅰ）求曲线C的直角坐标方程；
    （Ⅱ）写出直线l与曲线C交点的一个极坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=x-alnx，当x＞1时，f（x）＞0恒成立，则实数a的取值范围是（　　）
    A．（1，+∞）B．（-∞，1）C．（e，+∞）D．（-∞，e）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

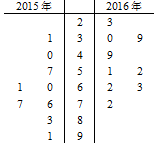    18．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，它是形成雾霾的原因之一．PM2.5日均值越小，空气质量越好.2012年2月29日，国家环保部发布的《环境空气质量标准》见表：
    PM2.5日均值k（微克）空气质量等级
    k≤35一级
    35＜k≤75二级
    k＞75超标
    针对日趋严重的雾霾情况，各地环保部门做了积极的治理．马鞍山市环保局从市区2015年11月～12月和2016年11月～12月的PM2.5检测数据中各随机抽取9天的数据来分析治理效果．样本数据如茎叶图所示（十位为茎，个位为叶）
    （Ⅰ）分别求两年样本数据的中位数和平均值，并以此推断2016年11月～12月的空气质量是否比2015年同期有所提高？
    （Ⅱ）在2015年的9个样本数据中随机抽取两天的数据，求这两天空气质量均超标的概率？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知集合P={x|-1≤x≤1}，M={a}，若P∩M=∅，则a取值范围是（　　）
    A．（-∞，-1]B．[1，+∞）C．[-1，1]D．（-∞，-1）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．将A，B，C，D这4名同学从左至右随机地排成一排，则“A与B相邻且A与C之间恰好有1名同学”的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{4}$C．$\frac{1}{6}$D．$\frac{1}{8}$

    查看答案和解析>>

    同步练习册答案