
(2014•泉州模拟)若函数y=f(x)满足:集合A={f(n)|n∈N*}中至少有三个不同的数成等差数列,则称函数f(x)是“等差源函数”,则下列四个函数中,“等差源函数”的个数是( )
①y=2x+1;
②y=log2x;
③y=2x+1;
④y=sin( x+
x+ )
)
A.1 B.2 C.3 D.4
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源:[同步]2014年湘教版选修1-2 7.1解方程与数系的扩充练习卷(解析版) 题型:?????
(2009•聊城一模)已知M={y|y=i2n,n∈N*}(其中i为虚数单位), ,P={x|x2>1,x∈R},则以下关系中正确的是( )
,P={x|x2>1,x∈R},则以下关系中正确的是( )
A.M∪N=P B.∁RM=P∪N C.P∩N=M D.∁R(P∩N)=∅
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 6.2工序流程图练习卷(解析版) 题型:填空题
(2008•奉贤区二模)某工程的工序流程图如图所示,则该工程总工时数为 天.
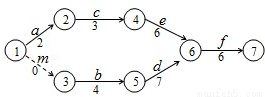
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 6.2工序流程图练习卷(解析版) 题型:选择题
下列判断不正确的是( )
A.画工序流程图类似于算法的流程图,要先把每一个工序逐步细化,按自上向下或自左到右的顺序
B.在工序流程图中可以出现循环回路,这一点不同于算法流程图
C.工序流程图中的流程线表示相邻两工序之间的衔接关系
D.工序流程图中的流程线都是有方向的指向线
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 5.1合情推理和演绎推理练习卷(解析版) 题型:?????
(2014•榆林模拟)甲,乙,丙,丁,戊5名学生进行某种劳动技术比赛决出第1名到第5名的名次(无并列).甲乙两名参赛者去询问成绩,回答者对甲说“很遗憾,你和乙都没有得到冠军”;对乙说“你当然不是最差的”.从这个人的回答中分析,5人的名次情况共有( )种.
A.54 B.48 C.36 D.72
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 5.1合情推理和演绎推理练习卷(解析版) 题型:?????
(2014•枣庄一模)在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:
(1)对任意a∈R,a*0=a;
(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).
则函数f(x)=(ex)*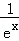 的最小值为( )
的最小值为( )
A.2 B.3 C.6 D.8
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 5.1合情推理和演绎推理练习卷(解析版) 题型:?????
(2015•洛阳一模)下面四个推导过程符合演绎推理三段论形式且推理正确的是( )
A.大前提:无限不循环小数是无理数;小前提:π丌是无理数;结论:π是无限不循环小数
B.大前提:无限不循环小数是无理数;小前提:π是无限不循环小数;结论:π是无理数
C.大前提:π是无限不循环小数;小前提:无限不循环小数是无理数;结论:π是无理数
D.大前提:π是无限不循环小数;小前提:π是无理数;结论:无限不循环小数是无理数
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 4.4一元线性回归案例练习卷(解析版) 题型:?????
(2014•郑州二模)某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
由表中数据,求得线性回归方程为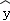 =﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
=﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
A.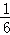 B.
B.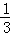 C.
C.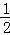 D.
D.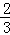
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 4.1随机对照实验案例练习卷(解析版) 题型:?????
(2009•东城区二模)在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取20个作为样本,有以下三种抽样方法:
①采用随机抽样法,将零件编号为00,01,…,99,抽签取出20个;
②采用系统抽样法,将所有零件分成20组,每组5个,然后每组随机抽取1个;
③采用分层抽样法,从一级品中随机抽取4个,从二级品中随机抽取6个,从三级品中随机抽取10个.
则下述判断中正确的是( )
A.不论采用何种抽样方法,这100个零件中每个被抽到的可能性均为
B.①、②两种抽样方法,这100个零件中每个被抽到的可能性均为 ;③并非如此
;③并非如此
C.①、③两种抽样方法,这100个零件中每个被抽到的可能性均为 ;②并非如此
;②并非如此
D.采用不同的抽样方法,这100个零件中每个被抽到的可能性是各不相同的
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com