
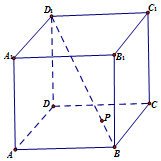
 正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )
正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )| A. | [1,3] | B. | [$\sqrt{6}$,3$\sqrt{6}$] | C. | [$\frac{3\sqrt{6}}{2}$,4$\sqrt{6}$] | D. | [$\sqrt{6}$,4$\sqrt{6}$] |
分析 分三种情况讨论f(x)的变换情况,利用相似三角形得出f(x)的值域.
解答 解:作平面ACB1和平面A1C1D,则BD1⊥平面AB1C,BD1⊥平面A1DC1,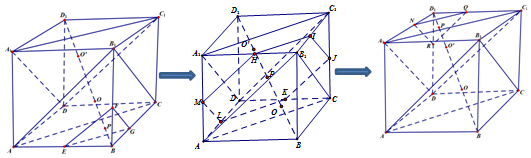
设B到平面ACB1的距离为d,则V${\;}_{B-A{B}_{1}C}$=V${\;}_{{B}_{1}-ABC}$,
∴$\frac{1}{3}×\frac{\sqrt{3}}{4}×$($\sqrt{6}$)2×d=$\frac{1}{3}×\frac{1}{2}×$($\sqrt{3}$)2×$\sqrt{3}$,解得d=1,
①当$x∈[{\frac{1}{3},1}]$时,截面多边形是三角形EFG,
由△EFG∽△AB1C得△EFG的周长为3$\sqrt{6}$x,∴3$\sqrt{6}$x∈$[{\sqrt{6},3\sqrt{6}}]$;
②当x∈(1,2)时,截面多边形是六边形HIJKLM,
设$\frac{HI}{{A}_{1}{C}_{1}}$=$\frac{{B}_{1}I}{{B}_{1}{C}_{1}}$=λ,则$\frac{IJ}{{B}_{1}C}$=$\frac{{C}_{1}I}{{B}_{1}{C}_{1}}$=1-λ,
∴HI+IJ=$\sqrt{6}$,
∴截面六边形的周长为$3\sqrt{6}$;
③当$x∈[{2,\frac{5}{2}}]$时,截面多边形是三角形NQR,
由①可知截面三角形周长范围为$[{\frac{{3\sqrt{6}}}{2},3\sqrt{6}}]$;
∴当x∈[$\frac{1}{3}$,$\frac{5}{2}$]时,f(x)的值域为[$\sqrt{6}$,3$\sqrt{6}$].
故选B.
点评 本题考查了棱柱的结构特征,属于中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举.这个伟大创举与我国古老的算法-“辗转相除法”实质一样.如图的程序框图即源于“辗转相除法”,当输入a=6102,b=2016时,输出的a=( )
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举.这个伟大创举与我国古老的算法-“辗转相除法”实质一样.如图的程序框图即源于“辗转相除法”,当输入a=6102,b=2016时,输出的a=( )| A. | 6 | B. | 9 | C. | 18 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .(2,16) | B. | .(-2,-16) | C. | .(4,16) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 63或126 | B. | 252 | C. | 120 | D. | 63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com