
分析 (1)根据题意,分2种情况讨论:①、取出的2个偶数不含0,②、取出的2个偶数含0,每种情况下先计算偶数、奇数的取法数目,再分析偶数、奇数之间的顺序,计算可得每种情况的四位数数目,由加法原理计算可得答案;
(1)根据题意,分2种情况讨论:①、取出的2个偶数不含0,用捆绑法分析可得四位数数目,②、取出的2个偶数含0,用间接法分析可得此时四位数数目,由加法原理计算可得答案.
解答 解:(1)根据题意,分2种情况讨论:
①、取出的2个偶数不含0,
偶数的取法有1种,奇数的取法有C32=3种,
将取出的4个数字全排列,有A44=24种情况,
则此时的四位数的数目有3×24=72个;
②、取出的2个偶数含0,
另一个偶数的取法有2种,奇数的取法有C32=3种,
除0之外的三个数中任选1个,安排在首位,有3种情况,
将剩余的3个数字全排列,有A33=6种情况,
则此时的四位数的数目有2×3×3×6=108个;
则可以有72+108=180个不同的四位数;
(2)根据题意,分2种情况讨论:
①、取出的2个偶数不含0,
偶数的取法有1种,奇数的取法有C32=3种,
将2个偶数看成一个整体,考虑其顺序,有A22=2种情况,
将这个整体与2个奇数全排列,有A33=6种情况,
则此时的四位数的数目有3×2×6=36个;
②、取出的2个偶数含0,
另一个偶数的取法有2种,奇数的取法有C32=3种,
将2个偶数看成一个整体,考虑其顺序,有A22=2种情况,
将这个整体与2个奇数全排列,有A33=6种情况,
其中0在首位的情况有2×3×2=6种,
则此时的四位数的数目有2×3×2×6-6=60个;
则可以有36+60=96个不同的四位数.
点评 本题考查排列、组合的综合应用,注意四位数的首位数字不能为0,在取出偶数时需要分类讨论.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,已知三棱锥S-ABC的三条侧棱长均为10,若∠BSC=α,∠CSA=β,∠ASB=γ且sin2$\frac{α}{2}+{sin^2}\frac{β}{2}={sin^2}\frac{γ}{2}$.
如图,已知三棱锥S-ABC的三条侧棱长均为10,若∠BSC=α,∠CSA=β,∠ASB=γ且sin2$\frac{α}{2}+{sin^2}\frac{β}{2}={sin^2}\frac{γ}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.
在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
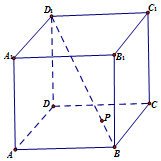 正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )
正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )| A. | [1,3] | B. | [$\sqrt{6}$,3$\sqrt{6}$] | C. | [$\frac{3\sqrt{6}}{2}$,4$\sqrt{6}$] | D. | [$\sqrt{6}$,4$\sqrt{6}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{3}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{3}{2}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com