
分析 (1)由题意,得$[\begin{array}{l}{3}&{a}\\{b}&{-2}\end{array}]$$[\begin{array}{l}{2}\\{3}\end{array}]$=$[\begin{array}{l}{3}\\{4}\end{array}]$得6+3a=3,2b-6=4,解得即可,
(2)求出矩阵A的逆矩阵为B,问题得以解决.
解答 解:(1)由题意,得$[\begin{array}{l}{3}&{a}\\{b}&{-2}\end{array}]$$[\begin{array}{l}{2}\\{3}\end{array}]$=$[\begin{array}{l}{3}\\{4}\end{array}]$得6+3a=3,2b-6=4,
所以a=-1,b=5.
(2)由(1),得矩阵A=$[\begin{array}{l}{3}&{a}\\{b}&{-2}\end{array}]$所由矩阵的逆矩阵公式得B=$[\begin{array}{l}{2}&{-1}\\{5}&{-3}\end{array}]$
B2=$[\begin{array}{l}{-1}&{1}\\{-5}&{4}\end{array}]$
点评 此题主要考查矩阵变换的问题,其中涉及到矩阵的乘法,题中是用一般方法求解,也可根据取特殊值法求解,具体题目具体分析找到最简便的方法.


科目:高中数学 来源: 题型:解答题
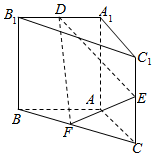 直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点.
直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
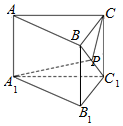 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面A1B1C1,∠ACB=90°,$AC=\sqrt{2},BC=C{C_1}=1,P$是BC1上一动点,则A1P+PC的最小值是$\sqrt{5}$.
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面A1B1C1,∠ACB=90°,$AC=\sqrt{2},BC=C{C_1}=1,P$是BC1上一动点,则A1P+PC的最小值是$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
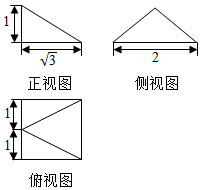
| A. | $3+\sqrt{3}$ | B. | $3+\sqrt{6}$ | C. | $1+2\sqrt{3}$ | D. | $1+2\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n-1 | B. | 2n | C. | 2n+1-1 | D. | 2n+1-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com