
分析 利用辅助角公式将函数进行化简结合三角函数的性质进行求解即可.
解答 解:f(x)=sin2x-cos2x=$\sqrt{2}$sin(2x-$\frac{π}{4}$),
∵$x∈[{0,\frac{π}{2}}]$,
∴2x∈[0,π],2x-$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{3π}{4}$],
sin(2x-$\frac{π}{4}$)∈[$-\frac{\sqrt{2}}{2}$,1],
$\sqrt{2}$sin(2x-$\frac{π}{4}$)∈[-1,$\sqrt{2}$],
故函数f(x)的值域为[-1,$\sqrt{2}$],
若将函数y=f(x)的图象向左平移a(a>0)个单位长度得到:
y=$\sqrt{2}$sin[2(x+a)-$\frac{π}{4}$]=$\sqrt{2}$sin(2x+2a-$\frac{π}{4}$),
若此时函数恰好关于直线$x=\frac{π}{4}$对称,
则2×$\frac{π}{4}$+2a-$\frac{π}{4}$=$\frac{π}{2}$+kπ,
即2a=$\frac{π}{4}$+kπ,
a=$\frac{π}{8}$+$\frac{kπ}{2}$,k∈Z,
故当k=0时,实数a的最小值为$\frac{π}{8}$,
故答案为:$[-1,\sqrt{2}]$;$\frac{π}{8}$
点评 本题主要考查三角函数值域以及三角函数图象平移的判断,根据三角函数的图象和性质是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进15m,至点C处测得顶端A的仰角为2θ,再继续前进5$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,则建筑物AE的高为$\frac{15}{2}$m.
如图在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进15m,至点C处测得顶端A的仰角为2θ,再继续前进5$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,则建筑物AE的高为$\frac{15}{2}$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
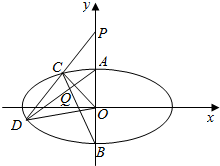 如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上、下顶点为A,B,点P(0,2)关于直线y=-x的对称点在椭圆M上,过点P的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间).
如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,上、下顶点为A,B,点P(0,2)关于直线y=-x的对称点在椭圆M上,过点P的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
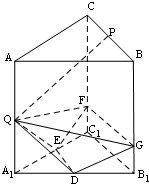 如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.
如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.
如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com