
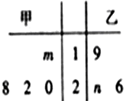
 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )| A. | $\frac{1}{8}$ | B. | 8 | C. | 9 | D. | $\frac{1}{9}$ |
分析 求平均数只要求出数据之和再除以总个数即可;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数,据此求出它们的中位数和平均数,即可求出答案.
解答 解:甲平均数是:$\frac{1}{4}$(10+m+20+22+28),
乙平均数是:$\frac{1}{3}$(19+n+20+26),
甲数据从小到大排列,位于中间的两个数的平均数是21,所以中位数21.
乙数据从小到大排列,位于中间的数是20+n,所以中位数20+n.
根据题意得:$\left\{\begin{array}{l}{\frac{10+m+20+22+28}{4}=\frac{19+n+20+26}{3}}\\{21=20+n}\end{array}\right.$,
∴m=8,n=1,
∴$\frac{m}{n}$=8.
故选:B.
点评 考查茎叶图、中位数与平均数的意义.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}>0$ | B. | (x1-x2)[f(x1)-f(x2)]>0 | ||
| C. | f(a)<f(x1)<f(x2)<f(b) | D. | $\frac{{x}_{1}-{x}_{2}}{f({x}_{1})-f({x}_{2})}>0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
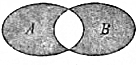 如图所示的韦恩图中,A,B中两非空集合,定义集合A?B为阴影部分表示的集合,若x,y∈R,A={x|y=ln(2x-x2)},B={y|y=ex,x>0},则A?B为( )
如图所示的韦恩图中,A,B中两非空集合,定义集合A?B为阴影部分表示的集合,若x,y∈R,A={x|y=ln(2x-x2)},B={y|y=ex,x>0},则A?B为( )| A. | {x|0<x<2} | B. | {x|x≤1或x≥2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0<x≤1或x≥2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
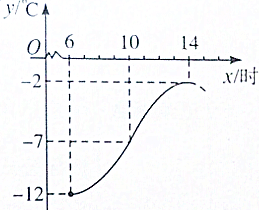 如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).
如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 200 | C. | 400 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com