
| A. | $\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}>0$ | B. | (x1-x2)[f(x1)-f(x2)]>0 | ||
| C. | f(a)<f(x1)<f(x2)<f(b) | D. | $\frac{{x}_{1}-{x}_{2}}{f({x}_{1})-f({x}_{2})}>0$ |
分析 根据函数单调性的等价条件进行判断即可.
解答 解:f(x)在[a,b]上是增函数,对于任意的x1,x2∈[a,b](x1≠x2),
则当x1<x2时,f(x1)<f(x2),此时满足$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}>0$,(x1-x2)[f(x1)-f(x2)]>0,$\frac{{x}_{1}-{x}_{2}}{f({x}_{1})-f({x}_{2})}>0$,
当x1>x2时,f(x1)>f(x2),此时满足$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}>0$,(x1-x2)[f(x1)-f(x2)]>0,$\frac{{x}_{1}-{x}_{2}}{f({x}_{1})-f({x}_{2})}>0$,
故不正确的是C,
故选:C
点评 本题主要考查函数单调性的应用,要求熟练掌握函数单调性的几种等价形式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{25}$ | B. | $\frac{12}{25}$ | C. | $\frac{7}{16}$ | D. | $\frac{11}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
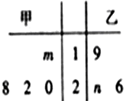 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )| A. | $\frac{1}{8}$ | B. | 8 | C. | 9 | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
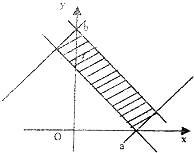 设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.
设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com