
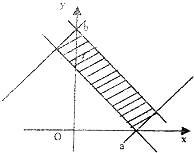
 设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.
设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.分析 (1)在同一坐标系内画出y≥|x-a|、y≤-|x|+b所表示的平面区域,数形结合可得使A∩B≠∅的a,b之间的关系;
(2)由(1)知,A∩B所表示的图形为矩形ACBD,求出矩形面积即可.
解答 解: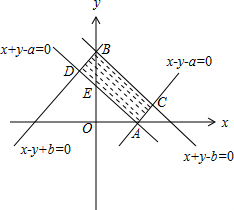 (1)不等式y≥|x-a|可化为$\left\{\begin{array}{l}{x-y-a≤0}\\{x≥a}\end{array}\right.$或$\left\{\begin{array}{l}{x+y-a≥0}\\{x<a}\end{array}\right.$,画出它所表示的平面区域如图所示,
(1)不等式y≥|x-a|可化为$\left\{\begin{array}{l}{x-y-a≤0}\\{x≥a}\end{array}\right.$或$\left\{\begin{array}{l}{x+y-a≥0}\\{x<a}\end{array}\right.$,画出它所表示的平面区域如图所示,
不等式y≤-|x|+b可化为$\left\{\begin{array}{l}{x-y-b≤0}\\{x≥0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y+b≥0}\\{x<0}\end{array}\right.$,
将其表示的平面区域与A表示的平面区域画在同一坐标系中,
如图所示,要使A∩B≠∅,只要b≥a;
(2)由(1)知,A∩B所表示的图形为矩形ACBD,
BE=b-a,在Rt△BDE中,∠DBE=45°,
∴BD=$\frac{\sqrt{2}}{2}(b-a)$,
又$AD=AE+DE=\sqrt{2}a+\frac{\sqrt{2}}{2}(b-a)=\frac{\sqrt{2}}{2}(b+a)$,
∴矩形面积S=$BD•AD=\frac{1}{2}({b}^{2}-{a}^{2})$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,正确作出图形是解答该题的关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}>0$ | B. | (x1-x2)[f(x1)-f(x2)]>0 | ||
| C. | f(a)<f(x1)<f(x2)<f(b) | D. | $\frac{{x}_{1}-{x}_{2}}{f({x}_{1})-f({x}_{2})}>0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
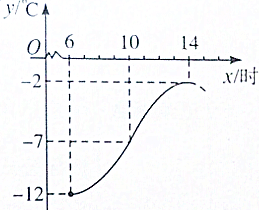 如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).
如图,牡丹江市某天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ<π|).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 200 | C. | 400 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com