
分析 设x1<x2,代入函数解析式化简f(x1)-f(x2),根据指数函数的单调性判断出符号,由函数单调性的定义即可得到结论.
解答 证明:解:设x1<x2,则f(x1)-f(x2)=$\frac{1-{2}^{{x}_{1}}}{2+{2}^{{x}_{1}+1}}$-$\frac{1-{2}^{{x}_{2}}}{2+{2}^{{x}_{2}+1}}$
=$\frac{(1-{2}^{{x}_{1}})(1+{2}^{{x}_{2}})-(1-{2}^{{x}_{2}})(1+{2}^{{x}_{1}})}{2(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$
=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$,
∵x1<x2,∴${2}^{{x}_{2}}>{2}^{{x}_{1}}$,则$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}>0$,
∴f(x1)-f(x2)>0,有f(x1)>f(x2),
∴f(x)在(-∞,+∞)上为减函数.
点评 本题考查函数的单调性的证明,即设值、作差、变形、定号、下结论,考查化简、变形能力,属于中档题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{25}$ | B. | $\frac{12}{25}$ | C. | $\frac{7}{16}$ | D. | $\frac{11}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
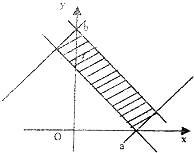 设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.
设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a、b是正数,且A∩B≠∅.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com