
分析 (1)利用商的关系、两角和的正弦公式、二倍角的正弦公式化简式子并求值;
(2)利用两角和的正切公式变形化简式子并求值.
解答 解:(1)式子=cos40°(1+$\sqrt{3}$•$\frac{sin10°}{cos10°}$)
=cos40°•$\frac{cos10°+\sqrt{3}sin10°}{cos10°}$=cos40°•$\frac{2sin40°}{cos10°}$
=$\frac{sin80°}{cos10°}$=$\frac{cos10°}{cos10°}$=1;
(2)式子=tan17°tan43°+tan30°[tan(17°+43°)(1-tan17°tan43°)
=tan17°tan43°+$\frac{\sqrt{3}}{3}•\sqrt{3}$(1-tan17°tan43°)
=1.
点评 本题考查三角函数化简求值,考查两角和的正切公式变形、商的关系、两角和的正弦公式、二倍角的正弦公式等,熟练掌握公式以及变形是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
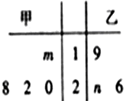 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的$\frac{m}{n}$=( )| A. | $\frac{1}{8}$ | B. | 8 | C. | 9 | D. | $\frac{1}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com