
分析 (1)由函数式,解得x2,令x2≥0,即可得到值域;(2)求得定义域,运用函数的单调性,可得值域;
(3)运用基本不等式,可得值域;运用二次函数的值域求法,可得所求值域.
解答 解:(1)y=$\frac{{x}^{2}-1}{{x}^{2}+1}$,即为x2=$\frac{-1-y}{y-1}$,
由x2≥0,解得-1≤y<1.
即值域为[-1,1);
(2)y=x-$\sqrt{1-2x}$(x≤$\frac{1}{2}$),
由y=x,y=-$\sqrt{1-2x}$在(-∞,$\frac{1}{2}$]递增,
即有函数y=x-$\sqrt{1-2x}$在(-∞,$\frac{1}{2}$]递增,则y≤$\frac{1}{2}$,
故值域为(-∞,$\frac{1}{2}$];
(3)由x>1,即x-1>0,
则y=$\sqrt{x-1}$+$\frac{1}{\sqrt{x-1}}$≥2,
当x=2时,取得最小值2.
则值域为[2,+∞);
(4)由x-x2=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$≤$\frac{1}{4}$,
可得0<$\sqrt{x-{x}^{2}}$≤$\frac{1}{2}$,
则y≥2,
即有值域为[2,+∞).
点评 本题考查函数的值域的求法,注意运用单调性和基本不等式等方法,考查运算能力,属于中档题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinA)>f(cosB) | B. | f(sinA)<f(cosB) | C. | f(sinA)>f(sinB) | D. | f(cosA)>f(cosB) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
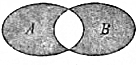 如图所示的韦恩图中,A,B中两非空集合,定义集合A?B为阴影部分表示的集合,若x,y∈R,A={x|y=ln(2x-x2)},B={y|y=ex,x>0},则A?B为( )
如图所示的韦恩图中,A,B中两非空集合,定义集合A?B为阴影部分表示的集合,若x,y∈R,A={x|y=ln(2x-x2)},B={y|y=ex,x>0},则A?B为( )| A. | {x|0<x<2} | B. | {x|x≤1或x≥2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0<x≤1或x≥2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com