
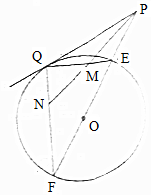
 如图所示,PQ为⊙O的切线,切点为Q,割线PEF过圆心O,且QM=QN.
如图所示,PQ为⊙O的切线,切点为Q,割线PEF过圆心O,且QM=QN.分析 (I)已知条件PQ为圆O的切线,联系切线的性质、弦切角定理,利用三角形相似,可得结论;
(II)求出∠PQF=120°,利用余弦定理求PF的长.
解答 (I)证明:因为PQ为圆O的切线,所以∠PFQ=∠PQE.…(1分)
又因为QM=QN,所以∠QNM=∠QMN,…(2分)
所以∠PNF=∠PMQ,…(3分)
所以△PNF∽△PMQ,…(4分)
所以$\frac{PF}{PQ}=\frac{NF}{MQ}=\frac{NF}{NQ}$,即PF•QN=PQ•NF;…(5分)
(II)解:因为QP=QF=$\sqrt{3}$,所以∠PFQ=∠QPF.…(6分)
又∠PFQ+∠QPF+∠PQE+∠EQF=180°,∠EQF=90°,…(7分)
所以∠PFQ=∠QPF=30°,∠PQF=120°,…(8分)
由余弦定理,得PF=$\sqrt{3+3-2•\sqrt{3}•\sqrt{3}•(-\frac{1}{2})}$=3.…(10分)
点评 本题考查圆周角定理、弦切角定理、余弦定理、圆的性质,以及考查逻辑四维能力、推理理论能力、转化能力、运算求解能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 1 | 2 | 3 |
| f(x) | 2 | 3 | 1 |
| x | 1 | 2 | 3 |
| g(x) | 3 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com