
分析 (1)利用条件,再写一式,两式相减,即可证明数列{an}是等比数列
(2)若$\lim_{n→∞}$Sn=1,$\lim_{n→∞}$[1-$(\frac{t}{t-1})^{n}$]=1,可得0<|$\frac{t}{t-1}$|<1,即可求实数t的取值范围.
解答 (1)证明:∵Sn=1+tan,
∴n≥2时,Sn-1=1+tan-1,
两式相减可得an=tan-tan-1,
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{t}{t-1}$,
∴数列{an}是等比数列;
(2)解:由题意,S1=1+ta1,∴a1=$\frac{1}{1-t}$,∴an=$\frac{1}{1-t}•(\frac{t}{t-1})^{n-1}$,
若$\lim_{n→∞}$Sn=1,则$\lim_{n→∞}$[1-$(\frac{t}{t-1})^{n}$]=1,
∴0<|$\frac{t}{t-1}$|<1,
∴$t<\frac{1}{2}$,
∵t≠1且t≠0,
∴$t<\frac{1}{2}$,且t≠0.
点评 本题考查等比数列的证明,考查数列的极限,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{21}{16}$ | B. | -$\frac{{3\sqrt{7}}}{8}$ | C. | -$\frac{{3\sqrt{7}}}{16}$ | D. | $\frac{{3\sqrt{7}}}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
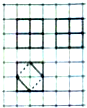 如图,网格纸上小正方形的边长为1,粗线画出的是由正方形切割而成的几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是由正方形切割而成的几何体的三视图,则该几何体的体积为( )| A. | $\frac{11}{2}$ | B. | $\frac{13}{2}$ | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
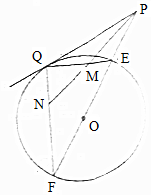 如图所示,PQ为⊙O的切线,切点为Q,割线PEF过圆心O,且QM=QN.
如图所示,PQ为⊙O的切线,切点为Q,割线PEF过圆心O,且QM=QN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com