
| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
分析 (I)由所给数据看出,年需求量与年份之间是近似直线上升,做出平均数,利用最小二乘法做出b,a,写出线性回归方程.
(II)把所给的x的值代入线性回归方程,求出变化以后的预报值,得到结果.
解答 解:(I)由所给数据看出,年需求量与年份之间是近似直线上升,下面来配回归直线方程,为此对数据预处理如下:
| 年份-2006 | -4 | -2 | 0 | 2 | 4 |
| 需求量-257 | -21 | -11 | 0 | 19 | 29 |
点评 本题考查回归分析的基本思想及其初步应用,考查回归方程的意义和求法,考查数据处理的基本方法和能力,考查利用统计思想解决实际问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | 若随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=0.21 | |
| B. | 若n组数据(x1,y1)…(xn,yn)的散点都在y=-2x+1上,则相关系数r=-1 | |
| C. | “x0为函数f(x)的极值点”是“f′(x0)=0”的充分不必要条件 | |
| D. | 若随机变量ξ服从二项分布:ξ~B(5,$\frac{1}{5}$),则Eξ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
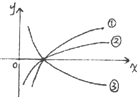 已知三个对数函数:y=logax,y=logbx,y=logcx,它们分别对应如图中标号为①②③三个图象 则a、b、c的大小关系是( )
已知三个对数函数:y=logax,y=logbx,y=logcx,它们分别对应如图中标号为①②③三个图象 则a、b、c的大小关系是( )| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com