练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
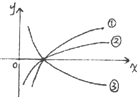
    9．已知三个对数函数：y=logax，y=logbx，y=logcx，它们分别对应如图中标号为①②③三个图象  则a、b、c的大小关系是（　　）
    A．a＜b＜cB．b＜a＜cC．c＜a＜bD．c＜b＜a

    分析 作直线y=1，其与四个函数图象的交点坐标分别是（a，1），（b，1），（c，1），由图象即可得出a、b、c大小关系．

    解答 解：如图作直线y=1，其与四个函数图象的交点坐标分别是（a，1），（b，1），（c，1），
    由图知四大小关系为以c＜a＜b．
    故选：C．

    点评 本题主要考查对数函数的性质，当函数值为1时，底数与真数相等，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．已知函数f（x）=x（lnx-2ax）有两个极值点，则实数a的取值范围是（　　）
    A．（-∞，$\frac{1}{4}$）B．（0，$\frac{1}{2}$）C．（0，$\frac{1}{4}$）D．（$\frac{1}{2}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知$0＜β＜α＜\frac{π}{2}$，且$cosα=\frac{5}{13}$，$cos（α-β）=\frac{4}{5}$．
    （Ⅰ）求$cos（α+\frac{π}{4}）$的值；                  
    （Ⅱ）求sin（α-β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

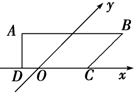    17．如图所示，ABCD是一平面图形的水平放置的斜二测直观图，在斜二测直观图中，ABCD是一直角梯形，AB∥CD，AD⊥CD，且BC与y轴平行，若AB=6，DC=4，AD=2，则这个平面图形的实际面积是20$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．在△ABC中，已知$a=9，c=2\sqrt{3}，B={150°}$，则边长b等于7$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

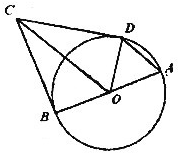    14．如图，已知AB是圆O的直径，BC与圆O相切与B，D为圆O上的一点，连接DC，DA，CO，DO，∠DAO+∠AOC=180°．
    （1）证明：△OBC≌△ODC；
    （2）证明：AD•OC=AB•OD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．某地最近十年粮食需求量逐年上升，如表是部分统计数据：
    年份20022004200620082010
    需求量（万吨）236246257276286
    （Ⅰ）利用所给数据求年需求量与年份之间的回归直线方程y=bx+a
    （Ⅰ）中所求出的直线方程预测该地2012年的粮食需求量．
    若（x1，y1 ），（x2，y2），…，（xn，yn ）为样本点，$\stackrel{∧}{y}$=bx+a，则 $\overline{x}$=$\frac{1}{n}$$\sum_{i=1}^{n}{x}_{1}$，$\overline{y}$=$\frac{1}{n}$$\sum_{i=1}^{n}{y}_{1}$
    b=$\frac{\sum_{i=1}^{n}（{x}_{1}-\overline{y}）（{y}_{1}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{1}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{1}{y}_{1}-n\overline{x}\overline{y}}{{x}_{i}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$
    说明：若对数据适当的预处理，可避免对大数字进行运算．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知$\frac{2}{x}+\frac{8}{y}$=1（x＞0，y＞0），则2x+y的最小值为（　　）
    A．18B．$12+8\sqrt{2}$C．$12+2\sqrt{2}$D．$12+4\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知△ABC内接于单位圆，且△ABC面积为$\frac{1}{2}$，则长为sinA，sinB，sinC的三条线段构成的三角形的面积为$\frac{1}{8}$．

    查看答案和解析>>

    同步练习册答案