
分析 (Ⅰ)利用同角三角函数基本关系式即可求得sinα的值,然后由两角和与差的余弦函数解答;
(Ⅱ)结合(α-β)的取值范围和sin2α+cos2α=1解答.
解答 解:(Ⅰ)∵$0<β<α<\frac{π}{2}$,
∴sinα>0,
∴$cosα=\frac{5}{13}$,
∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{12}{13}$,
∴$cos(α+\frac{π}{4})$=$\frac{\sqrt{2}}{2}$(cosα-sinα)=$\frac{\sqrt{2}}{2}$×($\frac{5}{13}$-$\frac{12}{13}$)=-$\frac{7\sqrt{2}}{26}$,即$cos(α+\frac{π}{4})=-\frac{{7\sqrt{2}}}{26}$;
(Ⅱ)∵$0<β<α<\frac{π}{2}$,
∴0<α-β<$\frac{π}{2}$.
∴sin(α-β)>0,
∴sin(α-β)=$\sqrt{1-co{s}^{2}(α-β)}$=$\sqrt{1-\frac{16}{25}}$=$\frac{3}{5}$,即$sin(α-β)=\frac{3}{5}$.
点评 本题主要考查了同角三角函数基本关系式,两角与差的正余弦函数公式在三角函数化简求值中的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=0.21 | |
| B. | 若n组数据(x1,y1)…(xn,yn)的散点都在y=-2x+1上,则相关系数r=-1 | |
| C. | “x0为函数f(x)的极值点”是“f′(x0)=0”的充分不必要条件 | |
| D. | 若随机变量ξ服从二项分布:ξ~B(5,$\frac{1}{5}$),则Eξ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x和y的相关系数为直线m的斜率 | |
| B. | x和y的相关系数为任意实数 | |
| C. | 当n为偶数时,分布在m两侧的样本点的个数一定相同 | |
| D. | 直线m过点$({\overline x,\overline y})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
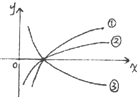 已知三个对数函数:y=logax,y=logbx,y=logcx,它们分别对应如图中标号为①②③三个图象 则a、b、c的大小关系是( )
已知三个对数函数:y=logax,y=logbx,y=logcx,它们分别对应如图中标号为①②③三个图象 则a、b、c的大小关系是( )| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com