
分析 (Ⅰ)由已知数列递推式可得${S}_{n}-{S}_{n-1}=\frac{2{{S}_{n}}^{2}}{2{S}_{n}-1}$(n≥2),整理后即可证明$\left\{{\frac{1}{S_n}}\right\}$是等差数列,求其通项公式后可得Sn的表达式;
(Ⅱ)构造函数f(n)=$\frac{(1+{S}_{1})(1+{S}_{2})…(1+{S}_{n})}{\sqrt{2n+1}}$,作商说明是增函数,求其最小值可得满足(1+S1)(1+S2)…(1+Sn)≥k$\sqrt{2n+1}$的k的最大值.
解答 (Ⅰ)证明:∵n≥2时,an=Sn-Sn-1,
∴由an=$\frac{2S_n^2}{{2{S_n}-1}}({n≥2})$,得${S}_{n}-{S}_{n-1}=\frac{2{{S}_{n}}^{2}}{2{S}_{n}-1}$,即Sn-1-Sn=2Sn•Sn-1,
由题意Sn≠0(n≥2),∴$\frac{1}{{S}_{n}}-\frac{1}{{S}_{n-1}}=2$(n≥2),
又S1=a1=1,∴$\left\{{\frac{1}{S_n}}\right\}$是以1为首项,以2为公差的等差数列,
则$\frac{1}{{S}_{n}}=1+2(n-1)=2n-1$,则${S}_{n}=\frac{1}{2n-1}$;
(Ⅱ)解:设f(n)=$\frac{(1+{S}_{1})(1+{S}_{2})…(1+{S}_{n})}{\sqrt{2n+1}}$,
则$\frac{f(n+1)}{f(n)}=\frac{(1+{S}_{n+1})\sqrt{2n+1}}{\sqrt{2n+3}}=\frac{2n+2}{\sqrt{2n+1}\sqrt{2n+3}}$=$\frac{\sqrt{4{n}^{2}+8n+4}}{\sqrt{4{n}^{2}+8n+3}}$>1.
故f(n)在n∈N*上递增,故使f(n)≥k恒成立,只需k≤f(n)min,
又$f(n)_{min}=f(1)=\frac{2\sqrt{3}}{3}$,∴k的最大值为$\frac{2\sqrt{3}}{3}$.
点评 本题考查数列递推式,考查了等差关系的确定,训练了恒成立问题的求解方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
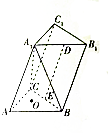 如图所示,在三棱柱ABC-A1B1C1中,底面△ABC是边长为6的等边三角形,点A1
如图所示,在三棱柱ABC-A1B1C1中,底面△ABC是边长为6的等边三角形,点A1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{4}$) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{4}$) | D. | ($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com